如圖是瑞典人科赫（Koch）在1906年構造的能夠描述雪花形狀的科赫雪花圖案．圖形的作法是，從一個正三角形開始，把每條邊分成三等份，然后以各邊的中間長度為底邊．分別向外作正三角形，再把“底邊”線段抹掉．反復進行這一過程，就會得到一個“雪花”樣子的曲線．這是一個極有特色的圖形：在圖形不斷變換的過程中，它的周長趨于無窮大，而其面積卻趨于定值．如果假定原正三角形邊長為
，則可算出下圖每步變換后科赫雪花的周長：
=3，
= ，
= ，…，則
= ．
科目：初中數學 來源：2014-2015學年浙江省金華市新世紀學校八年級上學期期中數學試卷（解析版） 題型：解答題
已知：如圖，AD=BC，AC=BD.
（1）求證：△ACD≌△BDC；
（2）求證：OD=OC.
查看答案和解析>>
科目：初中數學 來源：2014-2015學年浙江省紹興市六校九年級上學期第一次聯考數學試卷（解析版） 題型：填空題
反比例函數的圖象經過點P（2，1），則這個函數的圖象位于第 象限。
查看答案和解析>>
科目：初中數學 來源：2014-2015學年浙江省八年級上學期期中考試數學試卷（解析版） 題型：填空題
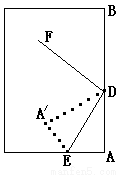
如圖，斜折一頁書的一角，使點A落在同一頁書內的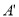
處，DE為折痕，作DF平分∠
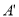DB，試猜想∠FDE=_______________.
查看答案和解析>>
科目：初中數學 來源：2014-2015學年浙江省八年級上學期期中考試數學試卷（解析版） 題型：解答題
（14分）如圖，△ABC中，點D是BC中點，連接AD并延長到點E，連接BE。
（1）若要使△ACD≌△EBD，應添上條件：__________
（2）證明上題：
（3）在△ABC中，若AB=5.AC=3，可以求得BC邊上的中線AD的取值范圍AD＜4.請看解題過程：
由△ACD≌△EBD得：AD=ED，BE=AC=3，因此AE＜AB+BE，即AE＜8，而AD=
AE，
則AD＜4，請參考上述解題方法，可求得AD＞m，則m的值為_______________.
（4）證明：直角三角形斜邊上的中線等于斜邊的一半。（提示：畫出圖形，寫出已知，求證，并加以證明）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，即為
；第三個在第二個的基礎上，多了其周長的 
，依此類推，則得到的第n個圖形的周長是第一個周長的
，即其周長是
．故答案為：
)÷5
的距離為2的點表示的數為（ ）
B．
C．
D．