
【題目】已知拋物線C:y=x2﹣3x+m,直線l:y=kx(k>0),當k=1時,拋物線C與直線l只有一個公共點.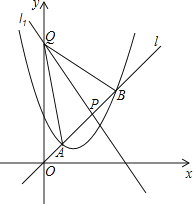
(1)求m的值;
(2)若直線l與拋物線C交于不同的兩點A,B,直線l與直線l1:y=﹣3x+b交于點P,且 ![]() +
+ ![]() =
= ![]() ,求b的值;
,求b的值;
(3)在(2)的條件下,設直線l1與y軸交于點Q,問:是否在實數k使S△APQ=S△BPQ?若存在,求k的值,若不存在,說明理由.
【答案】
(1)
解:當k=1時,拋物線C與直線l只有一個公共點,
∴直線l解析式為y=x,
∵ ![]() ,
,
∴x2﹣3x+m=x,
∴x2﹣4x+m=0,
∴△=16﹣4m=0,
∴m=4
(2)
解:如圖,

分別過點A,P,B作y軸的垂線,垂足依次為C,D,E,
則△OAC∽△OPD,∴ ![]() .
.
同理, ![]() .
.
∵ ![]() ,
,
∴ ![]() =2.
=2.
∴ ![]() =2.
=2.
∴ ![]() ,
,
即 ![]() .
.
解方程組 ![]() ,
,
得x=x= ![]() ,
,
即PD= ![]() .
.
由方程組 ![]() 消去y,得x2﹣(k+3)x+4=0.
消去y,得x2﹣(k+3)x+4=0.
∵AC,BE是以上一元二次方程的兩根,
∴AC+BE=k+3,AC×BE=4.
∴ ![]() .
.
解得b=8.
(3)
解:不存在.理由如下:
假設存在,
當S△APQ=S△BPQ時,有AP=PB,
于是PD﹣AC=PE﹣PD,
即AC+BE=2PD.
由(2)可知AC+BE=k+3,PD= ![]() ,
,
∴k+3=2× ![]() ,
,
即(k+3)2=16.
解得k=1(舍去k=﹣7).
當k=1時,A,B兩點重合,△BQA不存在.
∴不存在實數k使S△APQ=S△BPQ
【解析】(1)兩圖象有一個交點,則對應的方程組有一組解,即△=0,代入計算即可求出m的值;(2)作出輔助線,得到△OAC∽△OPD, ![]() +
+ ![]() =2,同理
=2,同理 ![]() +
+ ![]() =2,AC,BE是x2﹣(k+3)x+4=0兩根,即可;(3)由S△APQ=S△BPQ得到AC+BE=2PD,建立方程(k+3)2=16即可.此題是二次函數綜合題,主要考查了相似三角形的性質和判定,比例的性質,一元二次方程的根與系數的關系,解本題的關鍵是靈活運用根與系數的關系.
=2,AC,BE是x2﹣(k+3)x+4=0兩根,即可;(3)由S△APQ=S△BPQ得到AC+BE=2PD,建立方程(k+3)2=16即可.此題是二次函數綜合題,主要考查了相似三角形的性質和判定,比例的性質,一元二次方程的根與系數的關系,解本題的關鍵是靈活運用根與系數的關系.
【考點精析】認真審題,首先需要了解根與系數的關系(一元二次方程ax2+bx+c=0(a≠0)的根由方程的系數a、b、c而定;兩根之和等于方程的一次項系數除以二次項系數所得的商的相反數;兩根之積等于常數項除以二次項系數所得的商),還要掌握比例的性質(基本性質;更比性質(交換比例的內項或外項);反比性質(交換比的前項、后項);等比性質)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】某商場促銷,小魚將促銷信息告訴了媽媽,假設某一商品的定價為![]() ,并列出不等式為
,并列出不等式為![]() ,那么小魚告訴媽媽的信息是( )
,那么小魚告訴媽媽的信息是( )
A. 買兩件等值的商品可減100元,再打三折,最后不到1000元
B. 買兩件等值的商品可打三折,再減100元,最后不到1000元
C. 買兩件等值的商品可減100元,再打七折,最后不到1000元
D. 買兩件等值的商品可打七折,再減100元,最后不到1000元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面的對話:
MM:“請幫我稱些梨.”
售貨員:“您上次買的梨賣沒了,您試一試新進的蘋果,價格雖然比梨貴些,但蘋果營養價
值更高.”
MM:“好,我跟上次一樣,也買30元錢.”
對比兩次的電腦小票,MM發現:每千克蘋果的價格是梨的1.5倍,蘋果的重量比梨輕2.5
千克.
根據上面的對話和MM發現,分別求出蘋果和梨的單價.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點P、Q分別是邊長為4cm的等邊△ABC邊AB、BC上的動點,點P從頂點A,點Q從頂點B同時出發,且它們的速度都為1cm/s。
⑴連接AQ、CP交于點M,在點P、Q運動的過程中,∠CMQ的大小變化嗎?若變化,則說明理由,若不變,請直接寫出它的度數;
⑵點P、Q在運動過程中,設運動時間為t,當t為何值時,△PBQ為直角三角形?
⑶如圖2,若點P、Q在運動到終點后繼續在射線AB、BC上運動,直線AQ、CP交點為M,則∠CMQ的大小變化嗎?則說明理由;若不變,請求出它的度數。

查看答案和解析>>
科目:初中數學 來源: 題型:
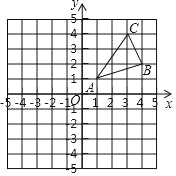
【題目】如圖,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4)
(1)若△A1B1C1與△ABC關于y軸成軸對稱,則△A1B1C1三個頂點坐標分別為A1_____,B1_____,C1_____
(2)在y軸上是否存在點Q.使得S△ACQ=![]() S△ABC,如果存在,求出點Q的坐標,如果不存在,說明理由;
S△ABC,如果存在,求出點Q的坐標,如果不存在,說明理由;
(3)在x軸上找一點P,使PA+PB的值最小,請直接寫出點P的坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在 Rt△ABC 中,∠C=90°,∠BAC=30°,點 D 是 BC 邊上的點,AB=18,將△ABC 沿直線 AD 翻折,使點 C 落在 AB 邊上的點 E 處,若點 P 是直線 AD 上的動點,則 BP+EP 的最小值是____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y= ![]() x2+bx+c經過△ABC的三個頂點,其中點A(0,1),點B(﹣9,10),AC∥x軸,點P是直線AC下方拋物線上的動點.
x2+bx+c經過△ABC的三個頂點,其中點A(0,1),點B(﹣9,10),AC∥x軸,點P是直線AC下方拋物線上的動點. 
(1)求拋物線的解析式;
(2)過點P且與y軸平行的直線l與直線AB、AC分別交于點E、F,當四邊形AECP的面積最大時,求點P的坐標;
(3)當點P為拋物線的頂點時,在直線AC上是否存在點Q,使得以C、P、Q為頂點的三角形與△ABC相似,若存在,求出點Q的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在直角坐標系xoy中,直線l:y=kx+b交x軸,y軸于點E,F,點B的坐標是(2,2),過點B分別作x軸、y軸的垂線,垂足為A、C,點D是線段CO上的動點,以BD為對稱軸,作與△BCD或軸對稱的△BC′D.
(1)當∠CBD=15°時,求點C′的坐標.
(2)當圖1中的直線l經過點A,且k=﹣ ![]() 時(如圖2),求點D由C到O的運動過程中,線段BC′掃過的圖形與△OAF重疊部分的面積.
時(如圖2),求點D由C到O的運動過程中,線段BC′掃過的圖形與△OAF重疊部分的面積.
(3)當圖1中的直線l經過點D,C′時(如圖3),以DE為對稱軸,作于△DOE或軸對稱的△DO′E,連結O′C,O′O,問是否存在點D,使得△DO′E與△CO′O相似?若存在,求出k、b的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的坐標系中,△ABC的三個頂點的坐標依次為A(﹣1,2),B(﹣4,1),C(﹣2,﹣2)
(1)請寫出△ABC關于x軸對稱的點A1、B1、C1的坐標;
(2)請在這個坐標系中作出△ABC關于y軸對稱的△A2B2C2;
(3)計算:△A2B2C2的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com