
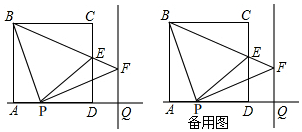
分析 (1)先判斷出AB=PQ,用同角的余角相等得出∠ABP=∠QPF,進(jìn)而得出△BAP≌△PQF,即可判斷出三角形BPF是等腰直角三角形即可;
(2)分三種情況,用三角形全等、角平分線定理和由運動的特點即可判斷出結(jié)論;
(3)先判斷出DGFQ是邊長為1的正方形,再用相似三角形的性質(zhì)得出EG,進(jìn)而得出DE,最后用勾股定理即可求出結(jié)論.
解答 解:(1)由運動知,AP=DQ,
∴PQ=PD+DQ=PD+AP=AD,
∵四邊形ABCD是正方形,
∴AB=AD,
∴AB=PQ,
∵FQ⊥AD,
∴∠PQF=∠BAD=90°,
∴∠APB+∠ABP=90°,
∵AP⊥PF,
∴∠APB+∠FPQ=90°,
∴∠ABP=∠QPF,
在△BAP和△PQF中,$\left\{\begin{array}{l}{∠ABP=∠QPF}\\{AB=PQ}\\{∠BAP=∠PQF}\end{array}\right.$,
∴△BAP≌△PQF,
∴PB=PF,AP=FQ=t,
∴△BPF是等腰直角三角形,
∴∠PBF=45°,
(2)如圖,
連接BD,
當(dāng)BP=BE時,
在Rt△ABP和Rt△CBE中,$\left\{\begin{array}{l}{BP=BE}\\{AB=BC}\end{array}\right.$,
∴Rt△ABP≌Rt△CBE,
∴∠ABP=∠CBE,
∵∠ABP+∠CBE=45°,
∴∠ABP=22.5°,
∵∠ABD=45°,
∴∠DBPP=22.5°=∠ABP,
∴AP是∠BAC的平分線,
∴$\frac{AB}{BD}=\frac{AP}{DP}$
∵BD=$\sqrt{2}$AB,AP=t,PD=AD-AP=6-t,
∴$\frac{AB}{\sqrt{2}AB}=\frac{t}{6-t}$,
∴t=6($\sqrt{2}$-1),
當(dāng)PB=PE時,由(1)知,PB=PF,
∴點F,E重合,
即:點E,F(xiàn),D重合,點P和A重合,
此時,t=0,
當(dāng)EB=EP時,∠BPE=∠EBP=45°,
∴∠BEP=90°,
∴點F和點D重合,
此時,點P和點D重合,
∴AP=AD=6,
∴t=6÷1=6.
即:當(dāng)△PBE為等腰三角形時,t的值為0或6($\sqrt{2}$-1)或6;
(3)如圖1, 過點F作FG⊥CD,
過點F作FG⊥CD,
∴∠DGF=90°,
∵∠GDQ=∠FQD=90°,
∴四邊形DGFQ是矩形,
由運動知,AP=DQ=FQ=1,
∴矩形DGFQ是邊長為1的正方形,
∴DG=1,
∴CG=CD-DG=5,
∵BC∥FG,
∴△BCE∽△FGE,
∴$\frac{BC}{FG}=\frac{CE}{GE}$,
∴$\frac{CE}{GE}=\frac{6}{1}$,
∴EG=$\frac{1}{7}$CG=$\frac{5}{7}$,
∴DE=DG+EG=1+$\frac{5}{7}$=$\frac{12}{7}$,
在Rt△EDP中,DP=AD-AP=5,
∴PE=$\sqrt{D{P}^{2}+D{E}^{2}}$=$\frac{37}{7}$.
點評 此題是四邊形綜合題,主要考查了全等三角形的性質(zhì)和判定,角平分線定理,矩形的判定和性質(zhì),正方形的判定和性質(zhì),相似三角形的判定和性質(zhì),解本題的關(guān)鍵是判斷出∠PBF=45°,是一道中等難度的中考常考題.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
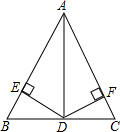 已知:如圖,△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB,DF⊥AC,垂足分別為E、F.求證:EB=FC.
已知:如圖,△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB,DF⊥AC,垂足分別為E、F.求證:EB=FC.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 +3(x-1)=x2-5x+1
+3(x-1)=x2-5x+1查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,四邊形ABCD、BEFG均為正方形.
如圖,四邊形ABCD、BEFG均為正方形.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com