
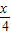 ×8)件.
×8)件.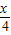 ×8),利用二次函數(shù)的最值求解即可.
×8),利用二次函數(shù)的最值求解即可.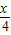 ×8)=1600
×8)=1600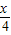 ×8),
×8),

 尖子生新課堂課時作業(yè)系列答案
尖子生新課堂課時作業(yè)系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數(shù)學 來源: 題型:
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源:不詳 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源:2009-2010學年福建省廈門市理工學院附中(杏南中學)九年級(上)期中數(shù)學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com