(1)證明:∵AD,BE是△ABC的兩條高
∴∠ADC=∠BEC=90°,
又∵∠C=∠C
∴△ACD∽△BCE
∴

=

,即CE•CA=CD•CB;
(2)解:∵

=

,∠C=∠C,EC=5,BC=13,
∴△CDE∽△ABC,
∴

=

=

.
分析:(1)先由AD,BE是△ABC的兩條高可知,∠ADC=∠BEC=90°,∠C=∠C,故可得出△ACD∽△BCE,根據相似三角形的對應邊成比例即可得出結論;
(2)根據(1)中

=

,∠C=∠C可得出△CDE∽△ABC,根據相似三角形的對應邊成比例即可得出結論.
點評:本題考查的是相似三角形的判定與性質,熟知相似三角形的對應邊成比例是解答此題的關鍵.

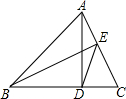 如圖,AD、BE是△ABC的兩條高.
如圖,AD、BE是△ABC的兩條高. 的值.
的值.