
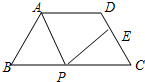
 如圖,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°P為底BC上一點(不與B、C重合)連接AP,過P點作PE交DC于E,使得∠APE=∠B.
如圖,等腰梯形ABCD中,AD∥BC,AD=3cm,BC=7cm,∠B=60°P為底BC上一點(不與B、C重合)連接AP,過P點作PE交DC于E,使得∠APE=∠B. (2)解:過點A作于AF∥CD交BC于點F,
(2)解:過點A作于AF∥CD交BC于點F,

科目:初中數學 來源: 題型:
 24、已知:如圖,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
24、已知:如圖,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2007•昌平區二模)已知:如圖,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=4
(2007•昌平區二模)已知:如圖,等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=4| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,等腰梯形ABCD中,AD∥BC,AB=CD,對角線BD平分∠ABC,且BD⊥DC,上底AD=3cm.
如圖,等腰梯形ABCD中,AD∥BC,AB=CD,對角線BD平分∠ABC,且BD⊥DC,上底AD=3cm.查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延長BC到E,使CE=AD.
如圖,等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥DC,延長BC到E,使CE=AD.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com