Question

兩圓的半徑分別是方程：x²-12x+17=0的兩根，圓心距為9，則兩圓的位置關系一定是    ．

Answer 1

【答案】分析：由兩圓的半徑分別是方程：x²-12x+17=0的兩根，根據根與系數的關系，即可求得兩圓的半徑的和與差，又由圓心距為9，根據兩圓位置關系與圓心距d，兩圓半徑R，r的數量關系間的聯系即可得出兩圓位置關系．
解答：解：設兩圓的半徑分別為R，r，
∵兩圓的半徑分別是方程：x²-12x+17=0的兩根，
∴R+r=12，R•r=17，
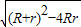
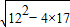
∴R-r===2，
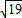
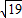
∵圓心距為9，2＜9＜12，
∴兩圓的位置關系一定是相交．
故答案為：相交．
點評：此題考查了圓與圓的位置關系，一元二次方程根與系數的關系．此題難度不大，解題的關鍵是注意掌握兩圓位置關系與圓心距d，兩圓半徑R，r的數量關系間的聯系．