
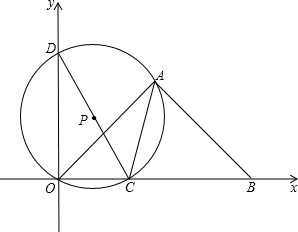
 (2013•樂清市模擬)如圖,等腰Rt△ABO的斜邊OB在x軸上,O是坐標原點,點A在第一象限內,BO=2,點C(t,0)是線段OB上一動點(不與O,B重合),△OAC的外接圓⊙P與y軸的另一交點為D.
(2013•樂清市模擬)如圖,等腰Rt△ABO的斜邊OB在x軸上,O是坐標原點,點A在第一象限內,BO=2,點C(t,0)是線段OB上一動點(不與O,B重合),△OAC的外接圓⊙P與y軸的另一交點為D.| OC2+OD2 |
| t2+(2-t)2 |
| 2 |
| 2-t |
| 2-t |
| t |
| 2 |
| t |
| (AE+AF)2-AE2-AF2 |
| 2 |
| 1 |
| 2 |
| 2t2-4t+4 |
| -t2+2t |
| 2(t2-2t)+4 |
| -(t2-2t) |
| 4 |
| -(t-1)2+1 |
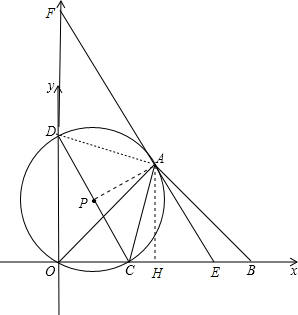 (1)證明:連結AD,如圖,
(1)證明:連結AD,如圖,
|
| OC2+OD2 |
| t2+(2-t)2 |
| 2(t-1)2+2 |
| 2 |
| 2 |
| 2-t |
| 2 |
| 2-t |
| 2-t |
| t |
| 2-t |
| t |
| 2 |
| 2-t |
| 2 |
| t |
| (AE+AF)2-AE2-AF2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2-t |
| 2 |
| t |
| 2t2-4t+4 |
| -t2+2t |
| 2(t2-2t)+4 |
| -(t2-2t) |
| 4 |
| -(t-1)2+1 |


科目:初中數學 來源: 題型:
 (2013•樂清市模擬)某校開展大課間活動,某班同學積極響應,某班同學參加大課間活動項目情況的扇形統計圖該班同學參加體育項目情況的扇形統計圖如圖所示,由圖可知參加人數最多的活動是( )
(2013•樂清市模擬)某校開展大課間活動,某班同學積極響應,某班同學參加大課間活動項目情況的扇形統計圖該班同學參加體育項目情況的扇形統計圖如圖所示,由圖可知參加人數最多的活動是( )查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•樂清市模擬)如圖,點D在△ABC的邊BC上,過點D作DF∥AB,交AC于點E,連結BF,已知BD:DC=1:2,DE:EF=1:3,則S△ABC:S△BDF=( )
(2013•樂清市模擬)如圖,點D在△ABC的邊BC上,過點D作DF∥AB,交AC于點E,連結BF,已知BD:DC=1:2,DE:EF=1:3,則S△ABC:S△BDF=( )查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•樂清市模擬)如圖,在四邊形ABCD中,AD∥BC,AD⊥AB,AB=BC=5,AD=1,E是AB所在直線上的一個動點,當
(2013•樂清市模擬)如圖,在四邊形ABCD中,AD∥BC,AD⊥AB,AB=BC=5,AD=1,E是AB所在直線上的一個動點,當| 4 |
| 5 |
5+
| ||
| 2 |
5-
| ||
| 2 |
| 4 |
| 5 |
5+
| ||
| 2 |
5-
| ||
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•樂清市模擬)如圖,在△ABC中,點O在AB邊上,以O為圓心的圓經過A,C兩點,交AB于點D,且2∠A+∠B=90°,
(2013•樂清市模擬)如圖,在△ABC中,點O在AB邊上,以O為圓心的圓經過A,C兩點,交AB于點D,且2∠A+∠B=90°,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com