
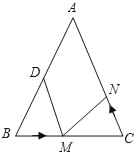
【題目】如圖在等腰△ABC中,AB=AC=20cm,BC=16cm,AD=BD.
(1)點M在底邊BC上且以6cm/s的速度由B點向C點運動,同時,點N在腰AC上且由C點向A點運動.
①如果點M與點N的運動速度相等,求經過多少秒后△BMD≌△CNM;
②如果點M與點N的運動速度不相等,當點N的運動速度為多少時,能夠使△BMD與△CNM全等?
(2)如果點N以②中的運動速度從點C出發,點M以6cm/s的速度從點B同時出發,都逆時針沿△ABC三邊運動,直接寫出當點M與點N第一次相遇時點M運動的路程.
【答案】(1)①1秒;②7.5厘米/秒;(2)![]() 秒.
秒.
【解析】
(1)①先求得BM=CN=6,MC=BD=10,然后根據等邊對等角求得∠B=∠C,最后根據SAS即可證明;
②因為VM≠VN,所以BM≠CN,又∠B=∠C,要使△BMD與△CNM全等,只能BM=CM=8,根據全等得出CN=BD=10,然后根據運動速度求得運動時間,根據時間和CN的長即可求得N的運動速度;
(2)因為VN>VM,只能是點N追上點M,即點N比點M多走AB+AC的路程,據此列出方程,解這個方程即可求得.
解:(1)①因為t=1(秒),
所以BM=CN=6(厘米)
∵AB=20,D為AB中點,
∴BD=10(厘米)
又∵MC=BC﹣BN=16﹣6=10(厘米)
∴MC=BD
∵AB=AC,
∴∠B=∠C,
在△BMD與△CNM中,
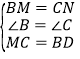 ,
,
∴△BMD≌△CNM(SAS),
∴經過1秒后△BMD≌△CNM.
②因為VM≠VN,
所以BM≠CN,
又因為∠B=∠C,
要使△BMD與△CNM全等,只能BM=CM=8,即△BMD≌△CMN,
故CN=BD=10.
所以點M、N的運動時間t=![]() (秒),
(秒),
此時VN=![]() =7.5(厘米/秒).
=7.5(厘米/秒).
(2)因為VN>VM,只能是點N追上點M,即點N比點M多走AB+AC的路程
設經過x秒后M與N第一次相遇,依題意得![]() x=6x+2×20,
x=6x+2×20,
解得x=![]() (秒)
(秒)
此時點M運動了![]() ×6=160(厘米)
×6=160(厘米)
又因為△ABC的周長為56厘米,160=56×2+48,
所以點M、N在AB邊上相遇,即經過了![]() 秒,點M與點N第一次在AB邊上相遇.
秒,點M與點N第一次在AB邊上相遇.


科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,O是對角線AC與BD的交點,M是BC邊上的動點(點M不與B、C重合),過點C作CN垂直DM交AB于點N,連結OM、ON、MN.下列五個結論:①△CNB≌△DMC;②![]() ;③ON⊥OM;④若AB=2,則
;③ON⊥OM;④若AB=2,則![]() 的最小值是1;⑤
的最小值是1;⑤![]() .其中正確結論是_________.(只填番號)
.其中正確結論是_________.(只填番號)

查看答案和解析>>
科目:初中數學 來源: 題型:
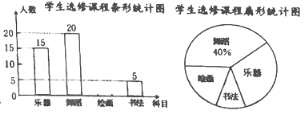
【題目】為發展學生的核心素養,培養學生的綜合能力,某學校計劃開設四門選修課:樂器、舞蹈、繪畫、書法,學校采取隨機抽樣的方法進行問卷調查(每個被調查的學生必須選擇而且只能選擇其中一門).對調查結果進行整理,繪制成如下兩幅不完整的統計圖.請結合圖中所給信息解答下列問題:
(1)本次調查的學生共有多少人?
(2)計算并將條形統計圖補充完整;
(3)該校共有學生2000人,估計該校約有多少人選修樂器課程?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P,Q是方格紙中的兩格點,請按要求畫出以PQ為對角線的格點四邊形.
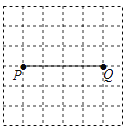
(1)在圖1中畫出一個面積最小的¨PAQB;
(2)在圖2中畫出一個四邊形PCQD,使其是軸對稱圖形而不是中心對稱圖形,且另一條對角線CD由線段PQ以某一格點為旋轉中心旋轉得到.注:圖1,圖2在答題紙上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知拋物線y=x2+bx+c過A,B,C三點,點A的坐標是(3,0),點C的坐標是(0,﹣3),動點P在拋物線上.
(1)求拋物線的解析式;
(2)若動點P在第四象限內的拋物線上,過動點P作x軸的垂線交直線AC于點D,交x軸于點E,垂足為E,求線段PD的長,當線段PD最長時,求出點P的坐標;
(3)是否存在點P,使得△ACP是以AC為直角邊的直角三角形?若存在,求出所有符合條件的點P的坐標;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是根據九年級某班50名同學一周的鍛煉情況繪制的條形統計圖,下面關于該班50名同學一周鍛煉時間的說法錯誤的是( )

A.平均數是6
B.中位數是6.5
C.眾數是7
D.平均每周鍛煉超過6小時的人數占該班人數的一半
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在不透明的口袋中,裝有3個分別標有數字1、2、3的小球,它們除標示的數字外完全相同,小紅、小明和小亮用這些道具做摸球游戲.游戲規則如下:由小紅隨機從口袋中摸出一個小球,記錄下數字,放回搖勻,再由小明隨機從口袋中摸出一個小球,記錄下數字,放回搖勻.如果兩人摸到的小球上數字相同,那么小亮獲勝;如果兩人摸到的小球上數字不同,那么小球上數字大的一方獲勝.
(1)請用樹狀圖或列表的方法表示一次游戲中所有可能出現的結果;
(2)這個游戲規則對三人公平嗎?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com