解:(1)設反比例函數解析式為y=

(k≠0),
由一次函數與反比例函數都經過A(-2,-1),
故將x=-2,y=-1代入反比例解析式得:-1=
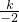
,
解得:k=2,
∴反比例函數解析式為y=

;
又B(n,2)在反比例函數圖象上,
∴將x=n,y=2代入反比例函數解析式得:2=

,
解得:n=1,即B(1,2),
設一次函數解析式為y=px+q(p≠0),
將A和B的坐標代入得:
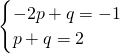
,
解得:
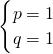
,
∴一次函數解析式為y=x+1;
(2)設一次函數與x軸交于C點,過A作AD⊥x軸于D點,過B作BE⊥x軸于E點,如圖所示:
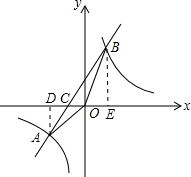
對應一次函數y=x+1,令y=0,解得:x=-1,故C(-1,0),即OC=1,
又A(-2,-1),B(1,2),
∴AD=1,BE=2,
則S
△OAB=S
△AOC+S
△BOC=

OC•AD+

OC•BE=

+1=

.
分析:(1)由一次函數與反比例函數圖象交于A和B兩點,故設出反比例函數解析式y=

(k≠0),將A的坐標代入求出k的值,確定出反比例解析式,將B的坐標代入反比例解析式中求出n的值,確定出B的坐標,設一次函數解析式為y=px+q(p≠0),將A與B的坐標代入一次函數解析式中,得到關于p與q的方程組,求出方程組的解得到p與q的值,確定出一次函數解析式;
(2)令(1)求出的一次函數解析式y=0,求出對應x的值,確定出C的坐標,得到OC的長,過A作AD⊥x軸于D點,過B作BE⊥x軸于E點,如圖所示,可得出AD即為A縱坐標的絕對值,BE為B縱坐標的絕對值,三角形AOB的面積=三角形AOC的面積+三角形BOC的面積,求出即可.
點評:此題考查了一次函數與反比例函數圖象的交點,待定系數法求函數解析式,坐標與圖形性質,以及三角形面積的求法,利用了數形結合及轉化的思想,靈活運用待定系數法是解本題的關鍵.

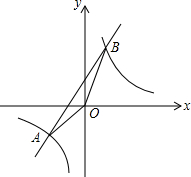 己知一次函數與反比例函數圖象都經過A(-2,-1)、B(n,2)兩點.
己知一次函數與反比例函數圖象都經過A(-2,-1)、B(n,2)兩點. (k≠0),
(k≠0),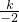 ,
, ;
; ,
,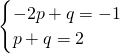 ,
,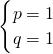 ,
,
 OC•AD+
OC•AD+ OC•BE=
OC•BE= +1=
+1= .
. (k≠0),將A的坐標代入求出k的值,確定出反比例解析式,將B的坐標代入反比例解析式中求出n的值,確定出B的坐標,設一次函數解析式為y=px+q(p≠0),將A與B的坐標代入一次函數解析式中,得到關于p與q的方程組,求出方程組的解得到p與q的值,確定出一次函數解析式;
(k≠0),將A的坐標代入求出k的值,確定出反比例解析式,將B的坐標代入反比例解析式中求出n的值,確定出B的坐標,設一次函數解析式為y=px+q(p≠0),將A與B的坐標代入一次函數解析式中,得到關于p與q的方程組,求出方程組的解得到p與q的值,確定出一次函數解析式;

 名校課堂系列答案
名校課堂系列答案 (任選一題,若兩題都選按得分最少的題記分,本題最高10分)
(任選一題,若兩題都選按得分最少的題記分,本題最高10分) 探索研究:
探索研究: (1)已知:如下圖,反比例函數的圖象經過點A、B,點A的坐標為(1,3),點B的縱坐標為1,點C的坐標為(2,0).
(1)已知:如下圖,反比例函數的圖象經過點A、B,點A的坐標為(1,3),點B的縱坐標為1,點C的坐標為(2,0).