
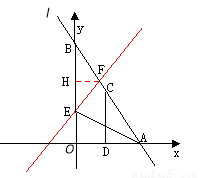
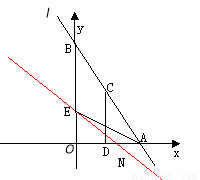
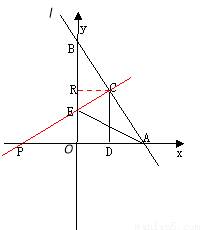
如圖,直線 :
: 分別與
分別與 軸、
軸、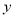 軸交于A、B兩點,點C線段AB上,作CD⊥x軸于D, CD=2OD, 點E線段OB上,且AE=BE;
軸交于A、B兩點,點C線段AB上,作CD⊥x軸于D, CD=2OD, 點E線段OB上,且AE=BE;


(1)填空:點C的坐標為( , );點E的坐標為( , );
(2)直線 過點E,且將△AOB分成面積比為1:2的兩部分,求直線
過點E,且將△AOB分成面積比為1:2的兩部分,求直線 的表達式;
的表達式;
(3)點P在x軸上運動,
①當PC+PE取最小值時,求點P的坐標及PC+PE的最小值;
②當PC-PE取最大值時,求點P的坐標及PC-PE的最大值;
見解析
【解析】
試題分析:(1)根據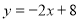 求出點A,B的坐標,A(4,0),B(0,8),所以OA=4,OB=8,設OD=m,則CD=2OD=2m,因為 CD⊥x軸,所以點C的坐標是(m,2m)代入
求出點A,B的坐標,A(4,0),B(0,8),所以OA=4,OB=8,設OD=m,則CD=2OD=2m,因為 CD⊥x軸,所以點C的坐標是(m,2m)代入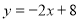 可求出點C的坐標,設OE=X,則AE=BE=8-x,在△OAE中,根據勾股定理可求出x的值,從而可得點E的坐標;(2)設直線m的表達式為
可求出點C的坐標,設OE=X,則AE=BE=8-x,在△OAE中,根據勾股定理可求出x的值,從而可得點E的坐標;(2)設直線m的表達式為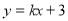 ,然后分情況討論(3)①求出點E關于X軸的對稱點E′坐標,然后求直線C E′與x軸的交點,即為點P;②直線CE與與x軸的交點即為點P.
,然后分情況討論(3)①求出點E關于X軸的對稱點E′坐標,然后求直線C E′與x軸的交點,即為點P;②直線CE與與x軸的交點即為點P.
試題解析:(1)點C( 2 , 4 );點E( 0 , 3 );
(2)設直線m的表達式為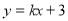
①如圖:當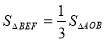 時,
時,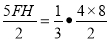
得FH=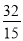 ,將
,將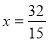 代入
代入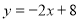 得
得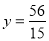
將點F(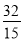 ,
,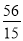 )代入
)代入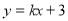 得
得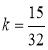 ,
,
所以直線m的表達式為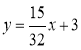
②如圖:當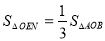 時,
時,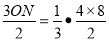 ,
,
得ON=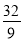 ,將點N(
,將點N(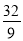 ,
,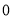 )代入
)代入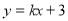 得
得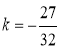 ,
,
所以直線m的表達式為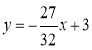
(3)①如圖:E關于X軸的對稱點E′坐標為(0,-3),
設直線CE′的表達式為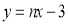 代入C(2,4)得;
代入C(2,4)得;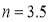 ,所以
,所以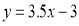
將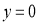 代入
代入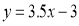 得
得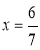
所以P的坐標為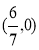
作E′Q⊥CD于Q,則CQ=OD=2,CQ=7
所以PC+PE的最小值= CE′=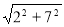 =
=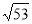
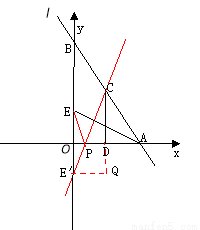
②如圖:設直線CE的表達式為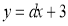 ,與x軸相交為p,
,與x軸相交為p,
代入C(2,4),得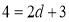 ,
,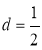
所以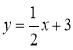 ,當
,當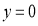 時,
時,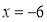 ;點P坐標為(-6,0),
;點P坐標為(-6,0),
作CR⊥y軸于R,則CR=OD=2,ER=1,
所以PC-PE的最大值= CE=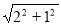 =
=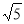
考點:1.一次函數與坐標軸的交點;2.求一次函數解析式;3.勾股定理;4.軸對稱-最短距離.


科目:初中數學 來源:2014-2015學年福建省、三中、城關小學九年級上學期期中聯考數學試卷(解析版) 題型:選擇題
下列圖形中,是中心對稱圖形,但不是軸對稱圖形的是( ).
A.正方形 B.矩形 C.菱形 D.平行四邊形
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省泉州市惠安第三教研片區九年級上學期期中考試數學試卷(解析版) 題型:填空題
在比例尺為1:1000000的地圖上,量得甲、乙兩地的距離約為3厘米,則甲、乙兩地的實際距離約為 千米.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省漳州立人學校八年級上學期期中考試數學試卷(解析版) 題型:選擇題
點A(2,-3)關于y軸的對稱點坐標是( )
A.(2,3) B.(-2,3) C.(-2,-3) D.(-3,2)
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期期中質量監測數學試卷(解析版) 題型:選擇題
不能判定四邊形ABCD是平行四邊形的條件是( )
A.∠A=∠C ∠B=∠D
B.AB∥CD AD=BC
C.AB∥CD ∠A=∠C
D.AB∥CD AB=CD
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省九年級上學期期中質量監測數學試卷(解析版) 題型:選擇題
如圖,在Rt⊿ABC中,∠C=90°, ∠B=22.5°, DE 垂直平分AB交BC于E, 若BE= , 則AC=( )
, 則AC=( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省龍巖市八年級上學期半期考試數學試卷(解析版) 題型:選擇題
如圖,在ΔABC中,AD⊥BC,CE⊥AB,垂足分別為D、E,AD、CE交于點H,已知EH=EB=3,AE=4,則CH的長為( )

A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com