
 小明從家去體育場鍛煉,同時,媽媽從體育場以50米/分的速度回家,小明到體育場后發現要下雨,立即返回,追上媽媽后,小明以250米/分的速度回家取傘,立即又以250米/分的速度折回接媽媽,并一同回家.如圖是兩人離家的距離y(米)與小明出發的時間x(分)之間的函數圖象.
小明從家去體育場鍛煉,同時,媽媽從體育場以50米/分的速度回家,小明到體育場后發現要下雨,立即返回,追上媽媽后,小明以250米/分的速度回家取傘,立即又以250米/分的速度折回接媽媽,并一同回家.如圖是兩人離家的距離y(米)與小明出發的時間x(分)之間的函數圖象.分析 (1)根據路程=速度×時間結合體育場離家3000米即可得出點C的坐標,根據點B、C的坐標利用待定系數法即可求出線段BC的表達式;
(2)根據點A、C的坐標利用待定系數法即可求出直線AC的表達式,由時間=路程÷速度結合點C的橫坐標即可得出點E的坐標,根據路程=速度×時間即可得出直線ED的表達式,聯立AC、ED的表達式成方程組,解之即可得出點D的坐標,再說出點D的實際意義即可;
(3)根據速度=路程÷時間即可求出小明去體育場的速度,由路程=速度×時間即可求出線段OB的表達式,根據OB、AC、BC的表達式結合小明與媽媽相距1500米即可得出關于x的一元一次方程,解之即可得出結論.
解答 解:(1)∵45×50=2250(米),3000-2250=750(米),
∴點C的坐標為(45,750).
設線段BC的函數表達式為y=kx+b(k≠0),
把(30,3000)、(45,750)代入y=kx+b,
$\left\{\begin{array}{l}{30k+b=3000}\\{45k+b=750}\end{array}\right.$,解得:$\left\{\begin{array}{l}k=-150\\ b=7500\end{array}\right.$,
∴線段BC的函數表達式y=-150x+7500(30≤x≤45).
(2)設直線AC的函數表達式為:y=k1x+b1,
把(0,3000)、(45,750)代入y=k1x+b1,
$\left\{\begin{array}{l}{{b}_{1}=3000}\\{45{k}_{1}+{b}_{1}=750}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=-50}\\{{b}_{1}=3000}\end{array}\right.$.
∴直線AC的函數表達式為y=-50x+3000.
∵750÷250=3(分鐘),45+3=48,
∴點E的坐標為(48,0).
∴直線ED的函數表達式y=250(x-48)=250x-12000.
聯立直線AC、ED表達式成方程組,
$\left\{\begin{array}{l}{y=-50x+3000}\\{y=250x-12000}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=50}\\{y=500}\end{array}\right.$,
∴點D的坐標為(50,500).
實際意義:小明將在50分鐘時離家500米的地方將傘送到媽媽手里.
(3)∵3000÷30=100(米/分鐘),
∴線段OB的函數表達式為y=100x(0≤x≤30),
由(1)線段BC的表達式為y=-150x+7500,(30≤x≤45)
當小明與媽媽相距1500米時,即-50x+3000-100x=1500或100x-(-50x+3000)=1500或(-150x+7500)-(-50x+3000)=1500,
解得:x=10或x=30,
∴當x為10或30時,小明與媽媽相距1500米.
故答案為:10或30.
點評 本題考查了一次函數的應用以及待定系數法求函數解析式,根據點的坐標利用待定系數法求出函數解析式是解題的關鍵.


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | 149×106 | B. | 1.49×108 | C. | 14.9×107 | D. | 0.149×109 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知長方形ABCD,E為BC邊上的一點,現將△ABE沿AE翻折,翻折后點B恰好落在邊DC上點F處.
如圖,已知長方形ABCD,E為BC邊上的一點,現將△ABE沿AE翻折,翻折后點B恰好落在邊DC上點F處.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
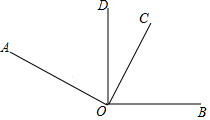 如圖,已知∠AOB=155°,∠AOC=∠BOD=90°.
如圖,已知∠AOB=155°,∠AOC=∠BOD=90°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com