
【題目】已知,在平面直角坐標系中,O為坐標原點,拋物線![]() 交
交![]() 軸于
軸于![]() 、
、![]() 兩點(
兩點(![]() 在
在![]() 軸負半軸上),交
軸負半軸上),交![]() 軸于點
軸于點![]() ,連接
,連接![]() ,
,![]() .
.
(1)求拋物線的解析式;
(2)![]() 為直線
為直線![]() 上方第一象限內一點,連接
上方第一象限內一點,連接![]() 、
、![]() ,
,![]() ,延長
,延長![]() 交
交![]() 軸于點
軸于點![]() ,設點
,設點![]() 的橫坐標為
的橫坐標為![]() ,點
,點![]() 的橫坐標為
的橫坐標為![]() ,求
,求![]() 與
與![]() 之間的函數關系式;(不要求寫出自變量
之間的函數關系式;(不要求寫出自變量![]() 的取值范圍)
的取值范圍)
(3)把線段![]() 沿直線
沿直線![]() 翻折,得到線段
翻折,得到線段![]() ,
,![]() 為第二象限內一點,連接
為第二象限內一點,連接![]() 、
、![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點,
上一點,![]() 于點
于點![]() ,射線
,射線![]() 交線段
交線段![]() 于點
于點![]() ,連接
,連接![]() 交
交![]() 于
于![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() ,若
,若![]() ,
,![]() ,設直線
,設直線![]() 與拋物線第一象限交點為
與拋物線第一象限交點為![]() ,求點
,求點![]() 坐標.
坐標.
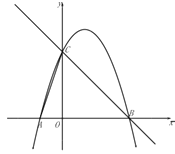
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (1,4)
(1,4)
【解析】
(1)根據拋物線解析式![]() 可求得點C坐標,再根據
可求得點C坐標,再根據![]() ,可求得點A坐標,再將點A坐標代入解析式即可求得;
,可求得點A坐標,再將點A坐標代入解析式即可求得;
(2)如圖,過點P作PH⊥x軸于H,過點B作BD⊥PR,證明∠PRB=∠PBR,則△PRB為等腰三角形,即可得到RH=HB,再代入各點橫坐標即可求得關系式;
(3)如圖,設![]() ,則
,則![]() ,所以
,所以![]() ,則E(﹣1,
,則E(﹣1,![]() ),
),
由![]() ,且BD為線段AB沿直線BC翻折所得,可知點D(3,4),求得
,且BD為線段AB沿直線BC翻折所得,可知點D(3,4),求得![]() ,
,
由FN⊥BE知![]() ,則
,則![]() ,可求直線FG的解析式為:
,可求直線FG的解析式為:![]() ,進而求得
,進而求得![]() ,因為
,因為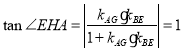 ,代入可求得
,代入可求得![]() ,則點G坐標為(3,2),所以直線AG的解析式為:
,則點G坐標為(3,2),所以直線AG的解析式為:![]() ,直線BE的解析式為:
,直線BE的解析式為:![]() ;再設點K(u,
;再設點K(u,![]() ),則
),則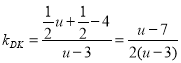 ,
,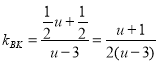 ,由
,由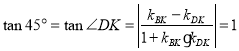 ,解得
,解得![]() ,則K(
,則K(![]() ,
,![]() ),直線BK的解析式為:
),直線BK的解析式為:![]() ,由點M為直線BK與拋物線的交點,聯立方程即可求得點M(1,4).
,由點M為直線BK與拋物線的交點,聯立方程即可求得點M(1,4).
解:(1)由拋物線![]() 可知,
可知,
點C(0,3),
∴OC=3,
∵![]() ,
,
∴OA=1,
∴A(﹣1,0),
將點A(﹣1,0)代入![]() ,
,
可求得:b=2,
∴拋物線的解析式為:![]()
(2)如圖,過點P作PH⊥x軸于H,過點B作BD⊥PR,
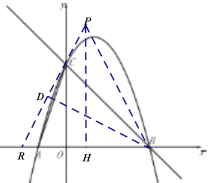
由(1)知拋物線的解析式為:![]() ,
,
∴可求得點B坐標為,(3,0),
∴OC=OB,
∴∠CBO=45°,
∵![]() ,
,
∴∠PBC=∠DBC,
∵∠PBR=∠PBC+∠CBO=45°+∠PBC,∠DRB=90°-∠DBR,而∠DBR=∠CBO-∠DBO,
∴∠DRB=90°-∠CBO+∠DBO=45°+∠DBO,
∴∠PRB=∠PBR,
∴△PRB為等腰三角形,RH=HB,
∵點![]() 的橫坐標為
的橫坐標為![]() ,點
,點![]() 的橫坐標為
的橫坐標為![]()
∴![]() ,
,
即![]() ;
;
(3)如圖,
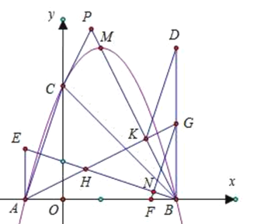
設![]() ,則
,則![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴E(﹣1,![]() ),
),
∵![]() ,BD為線段AB沿直線BC翻折所得,
,BD為線段AB沿直線BC翻折所得,
∴點D(3,4),
∴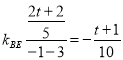 ,
,
∵FN⊥BE,
∴![]() ,
,
∴![]() ,
,
∴直線FG的解析式為:![]() ,
,
令![]() ,則
,則![]() (3,
(3,![]() ),
),
∴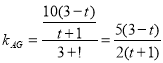
∵∠EHA=45°,
由直線的夾角公式得: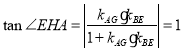 ,
,
∴![]() ,
,
∴![]() ,
,
化簡得:![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴G(3,2),
∴直線AG的解析式為:![]() ,
,
∴直線BE的解析式為:![]() ,
,
設點K(u,![]() ),
),![]() ,
,
∴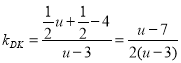 ,
,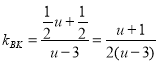 ,
,
由直線夾角公式得: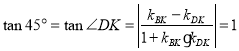 ,
,
即,![]() ,
,
∴![]() ,
,
化簡得:![]() 或
或![]() ,
,
解得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴K(![]() ,
,![]() ),
),
∴直線BK的解析式為:![]() ,
,
∵點M為直線BK與拋物線的交點,
∴聯立![]() ,
,
解得:![]() 或
或![]() (即為點B,舍去),
(即為點B,舍去),
所以點M(1,4).


科目:初中數學 來源: 題型:
【題目】隨著經濟的快速發展,環境問題越來越受到人們的關注,某校學生會為了解節能減排、垃圾分類知識
的普及情況,隨機調查了部分學生,調查結果分為“非常了解”“了解”“了解較少”“不了解”四類,
并將檢查結果繪制成下面兩個統計圖.
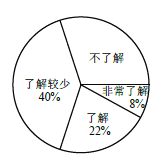
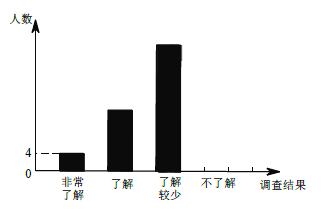
(1)本次調查的學生共有__________人,估計該校1200 名學生中“不了解”的人數是__________人.
(2)“非常了解”的4 人有![]() 兩名男生,
兩名男生,![]() 兩名女生,若從中隨機抽取兩人向全校做環保交流,請利用畫樹狀圖或列表的方法,求恰好抽到一男一女的概率.
兩名女生,若從中隨機抽取兩人向全校做環保交流,請利用畫樹狀圖或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
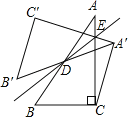
【題目】如圖,點D是Rt△ABC斜邊AB的中點,點E在邊AC上.△A'B′C′與△ABC關于直線BE對稱,連結A′C.且∠CA′C'=90°.若AC=4,BC=3.則AE的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,長、寬均為3,高為8的長方體容器,放置在水平桌面上,里面盛有水,水面高為6,繞底面一棱長進行旋轉傾斜后,水面恰好觸到容器口邊緣,圖2是此時的示意圖,則圖2中水面高度為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
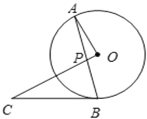
【題目】如圖,AB是⊙O的弦,點C為⊙O外一點,CO⊥OA,交AB于點P,連接BC,BC=PC.
(1)求證:BC是⊙O的切線;
(2)若⊙O的半徑為3,OP=1,求PC的長.
(3)在(2)的條件下,求BP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)計算:(![]() ﹣1)0+2sin30°-
﹣1)0+2sin30°-![]() +|﹣2017|;
+|﹣2017|;
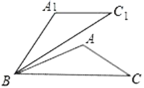
(2)如圖,在△ABC中,已知∠ABC=30°,將△ABC繞點B逆時針旋轉50°后得到△A1BC1,若∠A=100°,求證:A1C1∥BC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售一種商品,若將50件該商品按標價打八折銷售,比按原標價銷售這些商品少獲利200元.
![]() 求該商品的標價為多少元;
求該商品的標價為多少元;
![]() 已知該商品的進價為每件12元,根據市場調査:若按
已知該商品的進價為每件12元,根據市場調査:若按![]() 中標價銷售,該商場每天銷售100件;每漲1元,每天要少賣5件
中標價銷售,該商場每天銷售100件;每漲1元,每天要少賣5件![]() 那么漲價后要使該商品每天的銷售利潤最大,應將銷售價格定為每件多少元?最大利潤是多少?
那么漲價后要使該商品每天的銷售利潤最大,應將銷售價格定為每件多少元?最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com