
如圖(1)是某種臺燈的示意圖,燈柱BC固定垂直于桌面,AB是轉軸,可以繞著點B按順時針方向轉動,AB=10cm,BC=20cm,圓錐形燈罩的軸截面△APQ是等腰直角三角形,∠PAQ=90°,且PQ∥AB.轉動前,點A、B、C在同一直線上.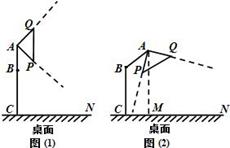
(1)轉動AB,如圖(2)所示,若燈心A到桌面的距離AM=25cm,求∠ABC的大小;
(2)繼續轉動AB,當光線AP第一次經過點C,求此時燈心A到桌面的距離AM長.(假設桌面足夠大)
(1)120°;(2)
解析試題分析:(1)過點B作BD⊥AM于D,求出BD的長度為5,因為AB=10,所以∠ABD=30°,再加上90°就是∠ABC的度數;
(2)過點B作BD⊥AC于D,由題意可知∠BAC=45°,AB=10cm,BC=20cm,即可求得BD、AD、CD的長,再由BC∥AM證得△ACM∽△CBD,根據相似三角形的性質即可求得結果.
(1)過點B作BD⊥AM于D
∵AM=25cm,
∴AD=5cm,
又∵AB=10cm,∠ADB=90°,
∴∠ABD=30°,
∴∠ABC=90°+30°=120°;
(2)過點B作BD⊥AC于D,
由題意可知∠BAC=45°,AB=10cm,BC=20cm
BD=AD=5 ,CD=
,CD=
∵BC∥AM
∴△ACM∽△CBD
∴AM= .
.
考點:解直角三角形的應用
點評:解直角三角形的應用是中考必考題,一般難度不大,正確作出輔助線構造直角三角形是解題關鍵.


 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇省無錫市宜興九年級5月中考適應性考試數學試卷(解析版) 題型:解答題
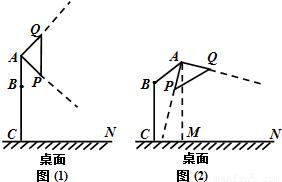
如圖(1)是某種臺燈的示意圖,燈柱BC固定垂直于桌面,AB是轉軸,可以繞著點B按順時針方向轉動,AB=10cm,BC=20cm,圓錐形燈罩的軸截面△APQ是等腰直角三角形,∠PAQ=90°,且PQ∥AB.轉動前,點A、B、C在同一直線上.

(1)轉動AB,如圖(2)所示,若燈心A到桌面的距離AM=25cm,求∠ABC的大小;
(2)繼續轉動AB,當光線AP第一次經過點C,求此時燈心A到桌面的距離AM長.(假設桌面足夠大)
查看答案和解析>>
科目:初中數學 來源:2010年浙江省嘉興市秀洲區中考數學二模試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com