
【題目】如圖,拋物線![]() 交
交![]() 軸于點
軸于點![]() 、
、![]() (
(![]() 在
在![]() 的左側),交
的左側),交![]() 軸于點
軸于點![]() ,且
,且![]() ,
,![]() .
.
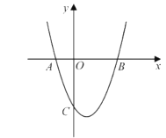
(1)求拋物線的解析式;
(2)點![]() 為第四象限拋物線上一點,過點
為第四象限拋物線上一點,過點![]() 作
作![]() 軸的平行線交
軸的平行線交![]() 于點
于點![]() ,設
,設![]() 點橫坐標為
點橫坐標為![]() ,線段
,線段![]() 的長度為
的長度為![]() ,求
,求![]() 與
與![]() 的函數關系式.(不要求寫出
的函數關系式.(不要求寫出![]() 的取值范圍)
的取值范圍)
(3)在(2)的條件下,![]() 為
為![]() 延長線上一點,且
延長線上一點,且![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的面積.
的面積.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)對于![]() ,令
,令![]() ,得
,得![]() ,從而點
,從而點![]() ,由
,由![]() 得到點
得到點![]() 將
將![]() 、
、![]() 代入
代入![]() ,由待定系數法即可拋物線的解析式為
,由待定系數法即可拋物線的解析式為![]() ;
;
(2)設![]() 由
由![]() ,
,![]() 可得直線
可得直線![]() 的解析式為
的解析式為![]() ,由
,由![]() 軸,故
軸,故![]() ,由此可得
,由此可得![]() ,從而
,從而![]() ;
;
(3)過點![]() 作
作![]() 的垂線交
的垂線交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于點
于點![]() ,過點
,過點![]() 做
做![]() ,延長
,延長![]() 交
交![]() 軸于點
軸于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() .由已知可得
.由已知可得![]() 、
、![]() 均為等腰直角三角形,從而
均為等腰直角三角形,從而![]() ,
,![]() ,由等式的性質可得
,由等式的性質可得![]() ,進而
,進而![]() ,由可得全等三角形的性質
,由可得全等三角形的性質![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() .由相似三角形的性質可得
.由相似三角形的性質可得![]() ,由三角形的面積可求得OM的值,在
,由三角形的面積可求得OM的值,在![]() 中,由正切的定義可求得t的值,由
中,由正切的定義可求得t的值,由![]() 即可得解.
即可得解.
(1)∵對于![]() ,
,
令![]() ,則
,則![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
將![]() 、
、![]() 代入
代入![]() ,
,
∴![]() ,解得,
,解得,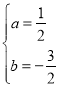
∴拋物線的解析式為![]() ;
;
(2)∵![]() 在拋物線
在拋物線![]() 上,設
上,設![]() ,
,
∵![]() ,
,![]() ,
,
∴直線![]() 的解析式為
的解析式為![]() ,
,
∵![]() 軸,
軸,
∴![]() 點的橫坐標與
點的橫坐標與![]() 點橫坐標相同,
點橫坐標相同,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)過點![]() 作
作![]() 的垂線交
的垂線交![]() 軸于點
軸于點![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于點
于點![]() ,過點
,過點![]() 做
做![]() ,延長
,延長![]() 交
交![]() 軸于點
軸于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() .
.
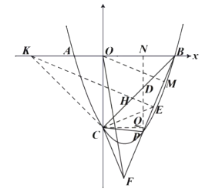
∵![]() ,
,![]() ,
,
∴![]() 、
、![]() 均為等腰直角三角形,
均為等腰直角三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴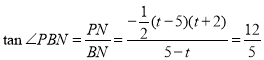 ,
,
∴![]() ,
,
∴![]()


科目:初中數學 來源: 題型:
【題目】平面內有一等腰直角三角板(∠ACB=90°)和一直線MN,過點C作CE⊥MN于點E,過點B作BF⊥MN于點F.當點E與點A重合時(如圖①),易證:AF+BF=2CE;當三角板繞點A順時針旋轉至圖②、圖③的位置時,上述結論是否仍然成立?若成立,請給予證明;若不成立,線段AF、BF、CE之間又有怎樣的數量關系,請直接寫出你的猜想,請直接寫出你的猜想,不需證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一種實驗用軌道彈珠,在軌道上行駛5分鐘后離開軌道,第一顆彈珠彈出后其速度![]() (米/分鐘)與時間
(米/分鐘)與時間![]() (分鐘)前2分鐘滿足二次函數
(分鐘)前2分鐘滿足二次函數![]() ,后3分鐘滿足反比例函數關系,如圖,軌道旁邊的測速儀測得彈珠1分鐘末的速度為2米/分鐘.
,后3分鐘滿足反比例函數關系,如圖,軌道旁邊的測速儀測得彈珠1分鐘末的速度為2米/分鐘.
(1)求第一顆彈珠的速度![]() (米/分鐘)與時間
(米/分鐘)與時間![]() (分鐘)之間的函數關系式;
(分鐘)之間的函數關系式;
(2)第一顆彈珠彈出1分鐘后,彈出第二顆彈珠,第二顆彈珠的運行情況與第一顆相同,直接寫出第二顆彈珠的速度![]() (米/分鐘)與彈出第一顆彈珠后的時間
(米/分鐘)與彈出第一顆彈珠后的時間![]() (分鐘)之間的函數關系式;
(分鐘)之間的函數關系式;
(3)當兩顆彈珠同時在軌道上時,第____分鐘末兩顆彈珠的速度相差最大,最大相差______;
(4)判斷當兩顆彈珠同時在軌道上時,是否存在某時刻速度相同?請說明理由,并指出可以通過解哪個方程求出這一時刻.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC 的頂點分別為 A(-2,2)、B(-4,5)、C(-5,1)和直線 m (直線 m 上各點的橫坐標都為 1).
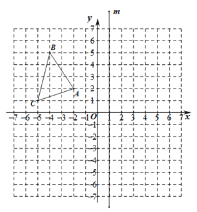
(1)作出△ABC 關于 ![]() 軸對稱的圖形△A1B1C1,并寫出點 A1 的坐標;
軸對稱的圖形△A1B1C1,并寫出點 A1 的坐標;
(2)作出點 C關于直線 m 對稱的點C2 , 并寫出點C2 的坐標;
(3)在![]() 軸上找一點P,使 PA+PC的值最小,請直接寫出點P的坐標.
軸上找一點P,使 PA+PC的值最小,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列每個圖形都是由一些黑點和一些白點按一定的規律組成的.
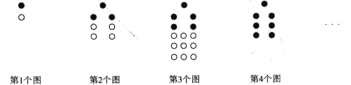
(1)根據規律,第4個圖中有 個白點;第![]() 個圖形中,白點和黑點總數的和為 (用
個圖形中,白點和黑點總數的和為 (用![]() 表示,
表示,![]() 為正整數);
為正整數);
(2)有沒有可能黑點比白點少2020個,如果有,求出此時![]() 的值;如果沒有,請說明理由.
的值;如果沒有,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在矩形AEFD中,點C為EF上一點,點B為FE的延長線上一點,連接CD、AB,![]() .
.
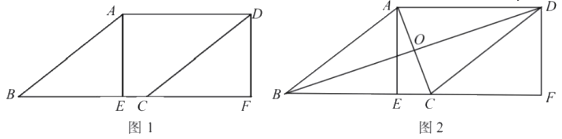
(1)如圖1,求證:![]() ;
;
(2)如圖2,連接BD、AC交于點![]() ,若
,若![]() ,在不添加任何輔助線的情況下,請直接寫出圖2中四個直角三角形,使寫出的每個三角形的面積等于四邊形
,在不添加任何輔助線的情況下,請直接寫出圖2中四個直角三角形,使寫出的每個三角形的面積等于四邊形![]() 的
的![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
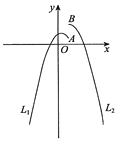
【題目】如圖,函數y=-x2+![]() x+c(-2020≤x≤1)的圖象記為L1,最大值為M1;函數y=-x2+2cx+1(1≤x≤2020)的圖象記為L2,最大值為M2.L1的右端點為A,L2的左端點為B,L1,L2合起來的圖形記為L.
x+c(-2020≤x≤1)的圖象記為L1,最大值為M1;函數y=-x2+2cx+1(1≤x≤2020)的圖象記為L2,最大值為M2.L1的右端點為A,L2的左端點為B,L1,L2合起來的圖形記為L.
(1)當c=1時,求M1,M2的值;
(2)若把橫、縱坐標都是整數的點稱為“美點”,當點A,B重合時,求L上“美點”的個數;
(3)若M1,M2的差為![]() ,直接寫出c的值.
,直接寫出c的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛慢車和一輛快車沿相同路線從A地到B地,所行駛的路程與時間的函數圖象如圖所示,下列說法正確的有( )
①快車追上慢車需6小時;
②慢車比快車早出發2小時;
③快車速度為46km/h;
④慢車速度為46km/h;
⑤AB兩地相距828km;
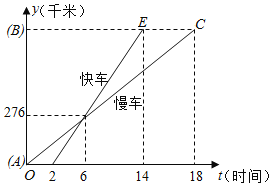
A.2個B.3個C.4個D.5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com