解:(1)答:PA+PB+PC的最小值為2a.
理由如下:
當點P與A重合時,PA+PB+PC=AC+AB
而AB>AC,故PA+PB+PC>2AC=2a
當點P在線段AC上運動時(不含A、C),PA+PB+PC=AC+PB,而PB>AC,故PA+PB+PC>2a
當P與C重合時,PA+PB+PC=AC+CB=2a,可見P在AC運動時PA+PB+PC的最小值是2a
同理,當點P在線段CB上運動時,PA+PB+PC的最小值為2a
當點P在線段AB上運動時,PA+PB+PC=AB+CP,而當CP⊥AB時,CP為最小值,其值為
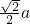
∴PA+PB+PC=AB+CP≥
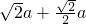
=

綜上,PA+PB+PC的最小值為2a;
(2)答:當P在AC上運動時(P與C點不重合),PA+PC<PB
當P與C點重合時,PA+PC=PB
當P在BC上運動時(P與C點不重合),PA+PC>PB
當P在AB上運動時,設P
0在線段AB上,且∠ACP
0=15°
當P在AP
0(不與P
0重合時)時,PA+PC<PB,當P在P
0B(不與P
0重合時)時,PA+PC>PB
當P與P
0重合時,PA+PC=PB,理由如下
當P在AC上運動時(P與C點不重合),PA+PC=AC=BC<PB
當P與C點重合時,PA+PC=AC=BC=PB
當P在BC上運動時(P與C點不重合),PA>AC=BC,而PB<BC
∴PA+PC>PB
如圖1,在線段AB上取DB=AP
0,連接CD,易證△AP
0C≌△BDC
則CP
0=CD,∠ACP
0=∠BCD=15°
∴∠P
0CD=60°∴△P
0CD是正三角形,即P
0D=P
0C,因此當P與P
0重合時,AP+PC=PB
當P在AP
0(不與P
0重合時)時,由于PC-P
0C<PP
0=AP
0-AP
∴PC+PA<P
0C+AP
0=P
0D+DB=P
0B<PB;
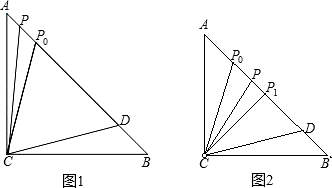
如圖2,當P在BP
0(不與P
0重合時)時,由于PP
0+PC>P
0C=P
0D
則PP
0+PC+AP
0>P
0C+AP
0=P
0D+DB=P
0B>PB
∴PA+PC>PB;
(3)

a<PA<

a或

a<PA<
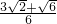
a.
理由如下:令P
1為AB的中點,不妨設P在AP
1上運動,要PA、PB、PC三條線段能構成三角形,須要PC-PA<PB<PA+PC
易見PB>PC>PA,則PC-PA<PB
由(2)知,要使PA+PC>PB,P應在P
0B,即∠PCA>15°
因為AP
0=AP
1-P
1P
0=

a-

a•cot60°=

a-

a=

a
即PA>
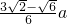
又知當P從在P
oB上從P
o向P
1運動時,PA,PB,PC構成的三角形從鈍角變為直角,再變為銳角
若設PA=x,則PB=

a-x,PC
2=(

a)
2+(

a-x)
2=a
2-

ax+x
2若PA、PB、PC構成的三角形是直角三角形,則有PB
2=PA
2+PC
2,即
(

a-x)
2=a
2-

ax+x
2,x
2+

ax-a
2=0,因x>0,所以x=

a
所以

a<PA<

a
同理可說明,當P在BP
1上運動,要PA、PB、PC三條線段若能構成鈍角三角形
須要

a<PA<
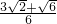
a
綜上可得:

a<PA<

a或

a<PA<
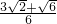
a.
分析:(1)由于本題P點的位置不確定,因此要分P與A重合,P在AC上,P與C重合,P在BC上,P在AB上五種情況進行討論.主要根據三角形三邊的關系進行求解;
(2)本題同(1)一樣,也要分類進行討論,也是根據三角形三邊的關系進行求解.要注意的是P在AB上運動時,由于無法直接用三角形三邊關系來求解,因此要通過構建特殊值來進行判斷,以CA、CB為邊C為頂點在兩邊各取一個15°角,設與AB的交點為P
0和D,那么不難得出△ACP
0≌△BCD,因此△P
0CD是個等邊三角形.
當P在AP
0上運動時,PA+PC<PA+AP
0=PA+BD=PB,綜合可得PA+PC<PB;
當P與P
0重合時,PC+PA=P0C+P0A=P
0D+BD=PB,即PA+PC=PB;
當P在P
0B上運動時,PA+PC=P0P+AP
0+PC=P0P+PC+BD,由于P
0P+PC>P
0C=P
0D,因此PA+PC=P
0P+PC+BD>P
0D+BD=PB;
(3)本題要考慮兩種情況:
要使PA,PB,PC構成銳角三角形,首先要滿足三邊能組成一個三角形;
要求出PA,PB,PC構成直角三角形時PA的值;
根據上面兩種情況求出的PA即可得出PA、PB、PC三條線段所構成銳角三角形時PA的取值范圍.
點評:本題主要考查了等腰直角三角形的性質、三角形三邊的關系、全等三角形的判定等知識點.綜合性強,難度大.

 已知△ABC是以AB為斜邊的等腰直角三角形,且AC=a,點P在△ABC的三條邊上運動,
已知△ABC是以AB為斜邊的等腰直角三角形,且AC=a,點P在△ABC的三條邊上運動,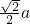
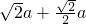 =
=

 a<PA<
a<PA< a或
a或 a<PA<
a<PA<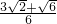 a.
a. a-
a- a•cot60°=
a•cot60°= a-
a- a=
a= a
a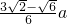
 a-x,PC2=(
a-x,PC2=( a)2+(
a)2+( a-x)2=a2-
a-x)2=a2- ax+x2
ax+x2 a-x)2=a2-
a-x)2=a2- ax+x2,x2+
ax+x2,x2+ ax-a2=0,因x>0,所以x=
ax-a2=0,因x>0,所以x= a
a a<PA<
a<PA< a
a a<PA<
a<PA<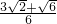 a
a a<PA<
a<PA< a或
a或 a<PA<
a<PA<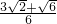 a.
a.

 如圖,已知△ABC,以AB為直徑的⊙O經過BC的中點D,DE⊥AC于E.
如圖,已知△ABC,以AB為直徑的⊙O經過BC的中點D,DE⊥AC于E. 已知△ABC是以AB為斜邊的等腰直角三角形,且AC=a,點P在△ABC的三條邊上運動,
已知△ABC是以AB為斜邊的等腰直角三角形,且AC=a,點P在△ABC的三條邊上運動, 24、如圖,直線CD經過線段AB的一個端點B,∠ABC=50°,點P為直線CD上一點;已知△PAB是以AB為底邊的等腰三角形,⊙O是以AB為直徑的圓.
24、如圖,直線CD經過線段AB的一個端點B,∠ABC=50°,點P為直線CD上一點;已知△PAB是以AB為底邊的等腰三角形,⊙O是以AB為直徑的圓.