
【題目】如圖①,直線![]() 與
與![]() 軸負半軸、
軸負半軸、![]() 軸正半軸分別交于
軸正半軸分別交于![]() 兩點,
兩點,![]() 的長度分別為
的長度分別為![]() 和
和![]() ,且滿足
,且滿足![]() .
.
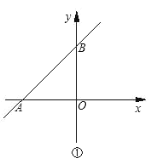
(1)![]() 是________三角形.
是________三角形.
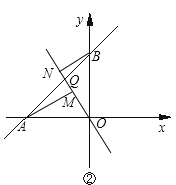
(2)如圖②,正比例函數![]() 的圖象與直線
的圖象與直線![]() 交于點
交于點![]() ,過
,過![]() 兩點分別作
兩點分別作![]() 于
于![]() ,
,![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長.
的長.
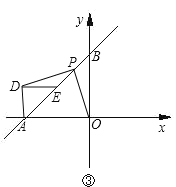
(3)如圖③,![]() 為
為![]() 上一動點,以
上一動點,以![]() 為斜邊作等腰直角
為斜邊作等腰直角![]() ,
,![]() 為
為![]() 的中點,連
的中點,連![]() ,試問:線段
,試問:線段![]() 是否存在某種確定的數量關系和位置關系?寫出你的結論并說明理由.
是否存在某種確定的數量關系和位置關系?寫出你的結論并說明理由.
【答案】(1)等腰直角;(2)6;(3)PO=PD且PO⊥PD.理由見解析.
【解析】
(1)已知a2-2ab+b2=0,化簡可得a=b,然后可得△AOB為等腰直角三角形;
(2)證明△MAO≌△NOB,得出AM=ON,然后求出MN的值;
(3)根據已知E為中點,聯想到延長DP到點C,使DP=PC,再連接OD、OC、BC,先證明△DEP≌△CBP得到邊角的等量關系,再證明△OAD≌△OBC,最后可得出△DOC為等腰直角三角形,從而得出結論.
解:(1)∵a2-2ab+b2=0,∴(a-b)2=0,
∴a=b,
∵∠AOB=90°,
∴△AOB為等腰直角三角形.
故答案為:等腰直角;
(2)∵∠MOA+∠MAO=90°,∠MOA+∠MOB=90°,
∴∠MAO=∠MOB,
∵AM⊥OQ,BN⊥OQ,
∴∠AMO=∠BNO=90°,
在△MAO和△BON中,
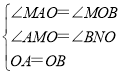 ,
,
∴△MAO≌△NOB(AAS),
∴AM=ON,
∴MN=ON-OM=AM-OM=6;
(3)PO=PD且PO⊥PD.理由如下:
如圖,延長DP到點C,使DP=PC,連接OD、OC、BC,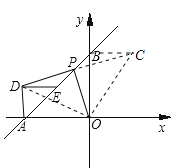
在△DEP和△CBP,
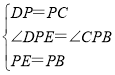 ,
,
∴△DEP≌△CBP(SAS),
∴CB=DE=DA,∠DEP=∠CBP=135°,
則∠CBO=∠CBP-∠ABO=135°-45°=90°,
又∵∠BAO=45°,∠DAE=45°,
∴∠DAO=90°,
在△OAD和△OBC,
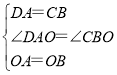 ,
,
∴△OAD≌△OBC(SAS),
∴OD=OC,∠AOD=∠COB,
∴∠COD=∠AOB=90°,
∴△DOC為等腰直角三角形,
∴PO=PD,且PO⊥PD.


科目:初中數學 來源: 題型:
【題目】每年暑假,都有許多驢友為實現自己的一個夢想,騎自行車丈量中國最美的公路川藏線。![]() 、
、![]() 兩個驢友團隊于同一天出發前往目的地拉薩。
兩個驢友團隊于同一天出發前往目的地拉薩。![]() 隊走317國道,結果30天到達。
隊走317國道,結果30天到達。![]() 隊走318國道,總路程比
隊走318國道,總路程比![]() 隊少200千米,且路況更好,平均每天比
隊少200千米,且路況更好,平均每天比![]() 隊多騎行20千米,結果
隊多騎行20千米,結果![]() 隊比
隊比![]() 隊提前8天到達拉薩.
隊提前8天到達拉薩.
(1)求318國道全程為多少千米?
(2)騎行過程中,![]() 隊每人每天平均花費150元。
隊每人每天平均花費150元。![]() 隊開始有3個人同行,計劃每人每天花費110元,后來又有幾個人加入隊伍,實際每增加1人時,每人每天的平均花費就減少5元。若最終
隊開始有3個人同行,計劃每人每天花費110元,后來又有幾個人加入隊伍,實際每增加1人時,每人每天的平均花費就減少5元。若最終![]() 、
、![]() 兩隊騎行的人數相同(均不超過10人),兩隊共花費了36900元,求兩驢友團隊各有多少人?
兩隊騎行的人數相同(均不超過10人),兩隊共花費了36900元,求兩驢友團隊各有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在平面直角坐標系中有三點![]() 、
、![]() 、
、![]() .請回答如下問題:
.請回答如下問題:
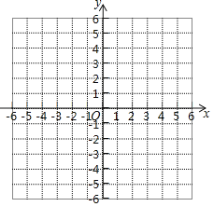
(1)在坐標系內描出![]() ;
;
(2)在坐標系中畫出![]() ,使它與
,使它與![]() 關于
關于![]() 軸對稱;
軸對稱;
(3)在![]() 軸上找一點
軸上找一點![]() ,使
,使![]() 的值最小,并求出此最小值.
的值最小,并求出此最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩位同學用圍棋子做游戲.如圖所示,現輪到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5個棋子組成軸對稱圖形,白棋的5個棋子也成軸對稱圖形.則下列下子方法不正確的是【 】.[說明:棋子的位置用數對表示,如A點在(6,3)]

A.黑(3,7);白(5,3) B.黑(4,7);白(6,2)
C.黑(2,7);白(5,3) D.黑(3,7);白(2,6)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】六一期間,某公園游戲場舉行“迎奧運”活動.有一種游戲的規則是:在一個裝有![]() 個紅球和若干個白球(每個球除顏色外其他相同)的袋中,隨機摸一個球,摸到一個紅球就得到一個奧運福娃玩具.已知參加這種游戲活動為
個紅球和若干個白球(每個球除顏色外其他相同)的袋中,隨機摸一個球,摸到一個紅球就得到一個奧運福娃玩具.已知參加這種游戲活動為![]() 人次,公園游戲場發放的福娃玩具為
人次,公園游戲場發放的福娃玩具為![]() 個.
個.
![]() 求參加一次這種游戲活動得到福娃玩具的概率;
求參加一次這種游戲活動得到福娃玩具的概率;
![]() 請你估計袋中白球接近多少個?
請你估計袋中白球接近多少個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com