已知方程x3-(1+2•3m)x2+(5n+2•3m)x-5n=0.
(1)若n=m=0,求方程的根;
(2)找出一組正整數n,m,使得方程的三個根均為整數;
(3)證明:只有一組正整數n,m,使得方程的三個根均為整數.
【答案】
分析:(1)若n=m=0,則方程化為x
3-3x
2+3x-1=0,即(x-1)
3=0.求解即可;
(2)設方程x
2-2•3
mx+5
n=0的兩個解為x
1,x
2.根據公式法求得后,再確定m,n的值;
(3)設9
m-5
n=k
2(其中k為整數),有9
m-k
2=5
n,即(3
m-k)(3
m+k)=5
n,再設
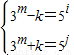
(其中i+j=n,i,j為非負整數),因此2•3
m=5
j(5
j-i+1),可得到2•3
m=5
n+1,然后討論m,n的取值.
解答:解:(1)若n=m=0,則方程化為x
3-3x
2+3x-1=0,即(x-1)
3=0.
所以x
1=x
2=x
3=1.
(2)方程化為(x-1)(x
2-2•3
mx+5
n)=0
設方程x
2-2•3
mx+5
n=0的兩個解為x
1,x
2.
則
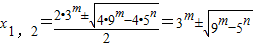
.
當m=n=1時,方程的三個根均為整數;
(3)設9
m-5
n=k
2(其中k為整數)
所以9
m-k
2=5
n,即(3
m-k)(3
m+k)=5
n,
不妨設
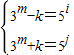
(其中i+j=n,i,j為非負整數),
因此:2•3
m=5
j(5
j-i+1),
又∵5不能整除2•3
m,
∴i=0,因此有2•3
m=5
n+1,
要使三根均為整數,則只有一組正整數m=n=1,此時x
1=x
2=1,x
3=5.
點評:此題運用了立方差公式和公式法,(3)的難度較大,注意分類討論.

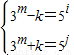 (其中i+j=n,i,j為非負整數),因此2•3m=5j(5j-i+1),可得到2•3m=5n+1,然后討論m,n的取值.
(其中i+j=n,i,j為非負整數),因此2•3m=5j(5j-i+1),可得到2•3m=5n+1,然后討論m,n的取值.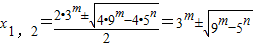 .
.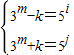 (其中i+j=n,i,j為非負整數),
(其中i+j=n,i,j為非負整數),

 優百分課時互動系列答案
優百分課時互動系列答案