
【題目】如圖,已知拋物線![]() 經過點A(3,1)與點B(0,4).
經過點A(3,1)與點B(0,4).

(1)求該拋物線的解析式及頂點坐標;
(2)在第三象限內的拋物線上有一點P,使得PA⊥AB,求點P的坐標;
(3)若點C(![]() ,
,![]() )在該拋物線上,當
)在該拋物線上,當![]() ≤
≤![]() ≤3時,1≤
≤3時,1≤![]() ≤5,請確定
≤5,請確定![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() , 頂點坐標為(1,5); (2)點P的坐標為(-2,-4); (3)
, 頂點坐標為(1,5); (2)點P的坐標為(-2,-4); (3) ![]() 的取值范圍是:-1≤
的取值范圍是:-1≤![]() ≤1.
≤1.
【解析】
(1)將![]() 代入
代入![]() ,解關于b、c的二元一次方程組,得到解析式進而求出頂點坐標;
,解關于b、c的二元一次方程組,得到解析式進而求出頂點坐標;
(2)分別過B與點P作![]() 軸的平行線BD、PE,過點A作
軸的平行線BD、PE,過點A作![]() 軸的垂線交BD于D、交PE于點E,證出AE=PE,設點P的坐標為
軸的垂線交BD于D、交PE于點E,證出AE=PE,設點P的坐標為![]() ,分別用含m的代數式表示出AE和PE的長,進而求出點P的坐標;
,分別用含m的代數式表示出AE和PE的長,進而求出點P的坐標;
(3)根據題意,分別求出q的最大值與最小值,從而確定q的取值范圍.
(1)將![]() 代入
代入![]() 得
得
![]()
解得![]()
∴![]() ,
,![]()
∴所求的拋物線的解析式為:![]() , 頂點坐標為(1,5)
, 頂點坐標為(1,5)
(2)如圖,分別過B與點P作![]() 軸的平行線BD、PE,過點A作
軸的平行線BD、PE,過點A作![]() 軸的垂線交BD于D、交PE于點E
軸的垂線交BD于D、交PE于點E
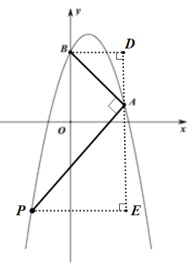
∵PA⊥AB
∴![]()
∴∠DAB+∠PAE=90°.
由A(3,1)、B(0,4)知BD=AD=3
∴∠DAB=45°
∴∠PAE=90°-∠DAB=90°-45°=45°
∴∠PAE=∠APE=45°
∴AE=PE
設點P的坐標為![]() 則
則
AE=![]()
PE=![]()
∴![]()
解得:![]() 或
或![]() (點P在第三象限,不合題意,舍去)
(點P在第三象限,不合題意,舍去)
∴![]() 時,
時,![]()
∴點P的坐標為(-2,-4).
(3)∵1≤n≤5且拋物線的頂點為(1,5)
∴區間包含頂點
∴![]() 的最大值為1
的最大值為1
在![]() 中,當
中,當![]() 時,
時,![]() 或者
或者![]()
∴![]() 的最小值為-1
的最小值為-1
∴![]() 的取值范圍是:-1≤
的取值范圍是:-1≤![]() ≤1.
≤1.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】教材呈現:下圖是華師版八年級上冊數學教材第94頁的部分內容.
線段垂直平分線
我們已知知道線段是軸對稱圖形,線段的垂直一部分線是線段的對稱軸,如圖直線![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,![]() 是
是![]() 上任一點,連結
上任一點,連結![]() 、
、![]() ,將線段
,將線段![]() 與直線
與直線![]() 對稱,我們發現
對稱,我們發現![]() 與
與![]() 完全重合,由此都有:線段垂直平分線的性質定理,線段垂直平分線上的點到線段的距離相等.
完全重合,由此都有:線段垂直平分線的性質定理,線段垂直平分線上的點到線段的距離相等.
已知:如圖,![]() ,垂足為點
,垂足為點![]() ,
,![]() ,點
,點![]() 是直線
是直線![]() 上的任意一點.
上的任意一點.
求證:![]() .
.
圖中的兩個直角三角形![]() 和
和![]() ,只要證明這兩個三角形全等,便可證明
,只要證明這兩個三角形全等,便可證明![]() (請寫出完整的證明過程)
(請寫出完整的證明過程)
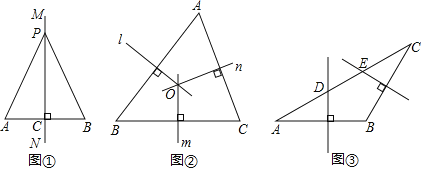
請根據教材中的分析,結合圖①,寫出“線段垂直平分線的性質定理”完整的證明過程,定理應用.
(1)如圖②,在![]() 中,直線
中,直線![]() 、
、![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 、
、![]() 的垂直平分線.
的垂直平分線.
求證:直線![]() 、
、![]() 、
、![]() 交于點.
交于點.
(2)如圖③,在![]() 中,
中,![]() ,邊
,邊![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,邊
,邊![]() 的垂直平分線交
的垂直平分線交![]() 于點
于點![]() ,若
,若![]() ,
,![]() ,則
,則![]() 的長為_______.
的長為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織全校學生進行了一次“社會主義核心價值觀”知識競賽,賽后隨機抽取了各年級部分學生成績進行統計,制作如下頻數分布表和頻數分布直方圖.請根據圖表中提供的信息,解答下列問題:
分數段( | 頻數 | 頻率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
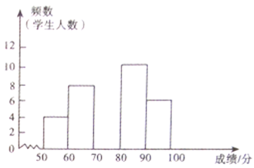
(1)請求出該校隨機抽取了____學生成績進行統計;
(2)表中![]() ____,
____,![]() ____,并補全直方圖;
____,并補全直方圖;
(3)若用扇形統計圖描述此成績統計分布情況,則分數段![]() 對應扇形的圓心角度數是___
對應扇形的圓心角度數是___![]() ;
;
(4)若該校共有學生8000人,請估計該校分數在![]() 的學生有多少人?
的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養殖場為了響應黨中央的扶貧政策,今年起采用“場內+農戶”養殖模式,同時加強對蛋雞的科學管理,蛋雞的產蛋率不斷提高,三月份和五月份的產蛋量分別是2.5萬kg與3.6萬kg,現假定該養殖場蛋雞產蛋量的月增長率相同.
(1)求該養殖場蛋雞產蛋量的月平均增長率;
(2)假定當月產的雞蛋當月在各銷售點全部銷售出去,且每個銷售點每月平均銷售量最多為0.32萬kg.如果要完成六月份的雞蛋銷售任務,那么該養殖場在五月份已有的銷售點的基礎上至少再增加多少個銷售點?
查看答案和解析>>
科目:初中數學 來源: 題型:
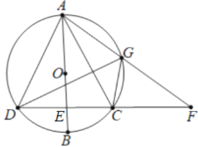
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于點E ,G是弧AC上的點,AG,DC延長線交于點F.
(1)求證:∠FGC=∠AGD.
(2)若BE=2,CD=8,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是一種推磨工具模型,圖2是它的示意圖,已知AB⊥PQ,AP=AQ=3dm,AB=12dm,點A在中軸線l上運動,點B在以O為圓心,OB長為半徑的圓上運動,且OB=4dm.
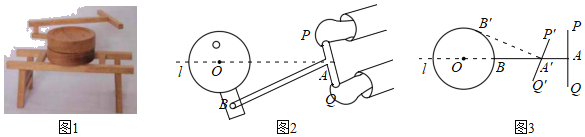
(1)如圖3,當點B按逆時針方向運動到B′時,A′B′與⊙O相切,則AA′=__dm.
(2)在點B的運動過程中,點P與點O之間的最短距離為__dm.
查看答案和解析>>
科目:初中數學 來源: 題型:
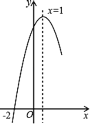
【題目】拋物線![]() 經過點(﹣2,0),且對稱軸為直線x=1,其部分圖象如圖所示.對于此拋物線有如下四個結論:
經過點(﹣2,0),且對稱軸為直線x=1,其部分圖象如圖所示.對于此拋物線有如下四個結論:
①![]() ;
;
②![]() >
>![]() ;
;
③若n>m>0,則![]() 時的函數值小于
時的函數值小于![]() 時的函數值;
時的函數值;
④點(![]() ,0)一定在此拋物線上.
,0)一定在此拋物線上.
其中正確結論的個數是( )
A.4個B.3個
C.2個D.1個
查看答案和解析>>
科目:初中數學 來源: 題型:
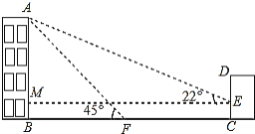
【題目】如圖,某辦公樓AB的右邊有一建筑物CD,在建設物CD離地面2米高的點E處觀測辦公樓頂A點,測得的仰角![]() =
=![]() ,在離建設物CD 25米遠的F點觀測辦公樓頂A點,測得的仰角
,在離建設物CD 25米遠的F點觀測辦公樓頂A點,測得的仰角![]() =
=![]() (B,F,C在一條直線上).
(B,F,C在一條直線上).
(1)求辦公樓AB的高度;
(2)若要在A,E之間掛一些彩旗,請你求出A,E之間的距離.(參考數據:![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com