【答案】
分析:(1)運用因式分解法解方程;(2)先將常數項5移到等號右邊,然后兩邊平方,將無理方程轉化為有理方程求解.
解答:解:(1)x
4+x
3+x+1=0
(x+1)x
3+x+1=0
(x+1)(x
3+1)=0
(x+1)
2(x
2-x+1)=0
則x+1=0,x=-1.
∴原方程的解為x=-1.
(2)
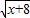
+
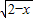
-5=0
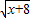
+
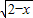
=5
x+8+2-x+2
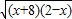
=25
2
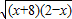
=15
x
2+6x+
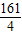
=0
∵△=36-161=-125<0,
∴原方程無解.
點評:(1)在將一個四項式分解因式時,應用分組分解法,這里是等項分組,還用到了立方和公式:a
3+b
3=(a+b)(a
2-ab+b
2).
(2)解無理方程的基本思想是通過兩邊平方,將無理方程轉化為有理方程,因此,解無理方程一定要檢驗.

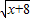 +
+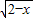 -5=0.
-5=0.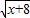 +
+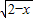 -5=0
-5=0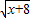 +
+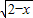 =5
=5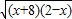 =25
=25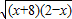 =15
=15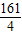 =0
=0
