Question

如圖，3個正方形拼成1個矩形，求∠EAD+∠EBD的度數．

Answer 1

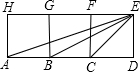
解：設正方形的邊長是1，則AC=2，BC=1，CE=，
∴=，=，
∴=，
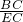
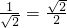
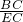
又∠BCE=∠ECA，
∴△ACE∽△ECB，
∴∠EAD=∠BEC，
∴∠EAD+∠EBD=∠BEC+∠EBD=∠ECD=45°．
分析：根據兩條對應邊的比相等，且夾角相等可以證明△ACE∽△ECB，再根據相似三角形的性質可以得到∠EAD=∠BEC，則∠EAD+∠EBD=∠BEC+∠EBD，再根據三角形的外角等于不相鄰的兩個內角的和，則所求的度數即為∠ECD的度數，根據正方形的性質即可求解．
點評：此題綜合運用了相似三角形的判定以及性質、正方形的性質、勾股定理．