陽光課堂課時優化作業系列答案科目：初中數學 來源： 題型：
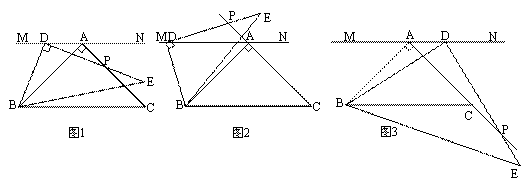
在等腰直角三角形ABC中，∠BAC=90°，AB=AC，直線MN過點A且MN∥BC.以點B為一銳角頂點作Rt△BDE，∠BDE=90°，且點D在直線MN上（不與點A重合）.如圖1，DE與AC交于點P，易證：BD=DP.(無需寫證明過程)
（1）在圖2中，DE與CA延長線交于點P，BD=DP是否成立？如果成立，請給予
證明，如果不成立，請說明理由；
（2）在圖3中，DE與AC延長線交于點P，BD與DP是否相等？請直接寫出你的結論，無需證明.
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，已知等腰三角形ABC的底角為30°，以BC為直徑的⊙O與底邊AB交于點D，過D作DE⊥AC，垂足為E．
（1）證明：DE為⊙O的切線；
（2）連接OE，若BC=4，求△OEC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，在△ABC和△BDE中，點C在邊BD上，邊AC交邊BE于點F．若AC=BD，AB=ED，BC=BE，則∠ACB等于（ ）
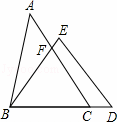
A．∠EDB B． ∠BED C．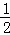 
∠AFB D． 2∠ABF
查看答案和解析>>
科目：初中數學 來源： 題型：
如圖，已知c＜0，拋物線y=x2+bx+c與x軸交于A（x1，0），B（x2，0）兩點（x2＞x1），與y軸交于點C．
（1）若x2=1，BC=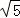
，求函數y=x2+bx+c的最小值；
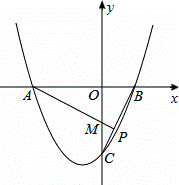
（2）過點A作AP⊥BC，垂足為P（點P在線段BC上），AP交y軸于點M．若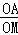
=2，求拋物線y=x2+bx+c頂點的縱坐標隨橫坐標變化的函數解析式，并直接寫出自變量的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
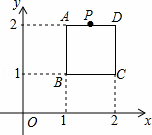
如圖，在平面直角坐標系中，邊長為1的正方形ABCD中，AD邊的中點處有一動點P，動點P沿P→D→C→B→A→P運動一周，則P點的縱坐標y與點P走過的路程s之間的函數關系用圖象表示大致是（ ）
A．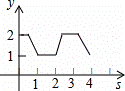 
B． 
C． 
D． 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
B． 
C． 
D． 1
（x+3）的解是