
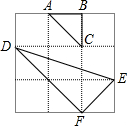
 在方格紙中,每個小方格的頂點叫做格點,以格點的連線為邊的三角形叫做格點三角形.在3×3的方格紙中
在方格紙中,每個小方格的頂點叫做格點,以格點的連線為邊的三角形叫做格點三角形.在3×3的方格紙中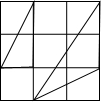
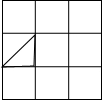
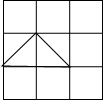

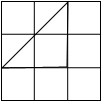
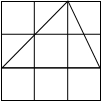
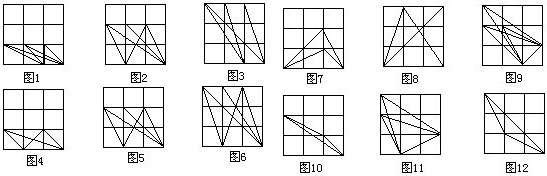 (3)面積不同或形狀不同的格點三角形的個數,可分類如下:
(3)面積不同或形狀不同的格點三角形的個數,可分類如下: :四個(圖9~10);
:四個(圖9~10); :三個(圖11~12);
:三個(圖11~12); :一個(圖13);
:一個(圖13);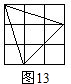 綜上所述,共得格點三角形29個;
綜上所述,共得格點三角形29個; ,
, ,2
,2 ,
, ,
, ,3
,3 ,于是面積不同或形狀不同的格點三角形的個數即可分類;
,于是面積不同或形狀不同的格點三角形的個數即可分類;

科目:初中數學 來源: 題型:
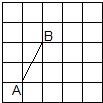 10、在如圖的方格紙中,每個小方格都是邊長為1的正方形,點A、B是方格紙中的兩個格點(即正方形的頂點),在這個5×5的方格紙中,找出格點C使△ABC的面積為2個平方單位,則滿足條件的格點C的個數是( )
10、在如圖的方格紙中,每個小方格都是邊長為1的正方形,點A、B是方格紙中的兩個格點(即正方形的頂點),在這個5×5的方格紙中,找出格點C使△ABC的面積為2個平方單位,則滿足條件的格點C的個數是( )查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解



查看答案和解析>>
科目:初中數學 來源: 題型:
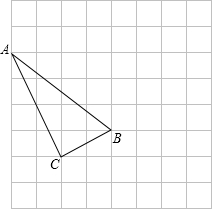 在如圖的方格紙中,每個小方格都是邊長為一個單位的正方形.
在如圖的方格紙中,每個小方格都是邊長為一個單位的正方形.查看答案和解析>>
科目:初中數學 來源: 題型:
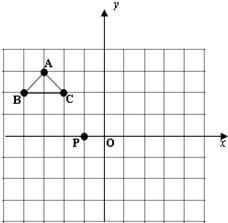 20、在建立平面直角坐標系的方格紙中,每個小方格都是邊長為1的小正方形,△ABC的頂點均在格點上,點P的坐標為(-1,0),請按要求畫圖與作答.
20、在建立平面直角坐標系的方格紙中,每個小方格都是邊長為1的小正方形,△ABC的頂點均在格點上,點P的坐標為(-1,0),請按要求畫圖與作答.查看答案和解析>>
科目:初中數學 來源: 題型:
 21、在如圖的方格紙中,每個小正方形的邊長都為1.
21、在如圖的方格紙中,每個小正方形的邊長都為1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com