日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 初中數學 > 題目詳情

閱讀材料：如圖，△ABC的周長為l，內切圓O的半徑為r，連結OA、OB、OC，△ABC被劃分為三個小三角形，用S△ABC表示△ABC的面積

∵S△ABC＝S△OAB＋S△OBC＋S△OCA

又∵S△OAB＝AB·r，S△OBC＝BC·r，S△OCA＝CA·r

∴S△ABC＝AB·r＋BC·r＋CA·r＝l·r(可作為三角形內切圓半徑公式)

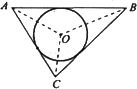
(1)理解與應用：利用公式計算邊長分為5、12、13的三角形內切圓半徑；

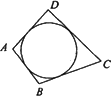
(2)類比與推理：若四邊形ABCD存在內切圓(與各邊都相切的圓，如圖)且面積為S，各邊長分別為a、b、c、d，試推導四邊形的內切圓半徑公式；

(3)拓展與延伸：若一個n邊形(n為不小于3的整數)存在內切圓，且面積為S，各邊長分別為a1、a2、a3、…an，合理猜想其內切圓半徑公式(不需說明理由)．

練習冊系列答案
相關習題

科目：初中數學 來源： 題型：閱讀理解

25、閱讀材料：
如圖（一），在已建立直角坐標系的方格紙中，圖形①的頂點為A、B、C，要將它變換到圖④（變換過程中圖形的頂點必須在格點上，且不能超出方格紙的邊界）．
例如：將圖形①作如下變換（如圖二）．
第一步：平移，使點C（6，6）移至點（4，3），得圖②；
第二步：旋轉，繞著點（4，3）旋轉180°，得圖③；
第三步：平移，使點（4，3）移至點O（0，0），得圖④．
則圖形①被變換到了圖④．

解決問題：
（1）在上述變化過程中A點的坐標依次為：
（4，6）→（
2
，
3
）→（
6
，
3
）→（
2
，
0
）
（2）如圖（三），仿照例題格式，在直角坐標系的方格紙中將△DEF經過平移、旋轉、翻折等變換得到△OPQ．（寫出變換步驟，并畫出相應的圖形）

查看答案和解析>>

科目：初中數學 來源： 題型：閱讀理解

精英家教網閱讀材料：
如圖1，過△ABC的三個頂點分別作出與水平線垂直的三條直線，外側兩條直線之間的距離叫△ABC的“水平寬”（a），中間的這條直線在△ABC內部線段的長度叫△ABC的“鉛垂高（h）”．我們可得出一種計算三角形面積的新方法：S△ABC=
12
ah，即三角形面積等于水平寬與鉛垂高乘積的一半．
解答下列問題：精英家教網
如圖2，拋物線頂點坐標為點C（-1，-4），交x軸于點A（-3，0），交y軸于點B．
（1）求拋物線和直線AB的解析式；
（2）點P是拋物線（在第三象限內）上的一個動點，連接PA，PB，當P點運動到頂點C時，求△CAB的鉛垂高CD及S△CAB；
（3）是否存在一點P，使S△PAB=S△CAB，若存在，求出P點的坐標；若不存在，請說明理由．

查看答案和解析>>

科目：初中數學 來源： 題型：閱讀理解

（2013•益陽）閱讀材料：如圖1，在平面直角坐標系中，A、B兩點的坐標分別為A（x1，y1），B（x2，y2），AB中點P的坐標為（xp，yp）．由xp-x1=x2-xp，得xp=
x1+x2
2
，同理yp=
y1+y2
2
，所以AB的中點坐標為(
x1+x2
2
，
y1+y2
2
)．由勾股定理得AB2=
.
x2-x1
  
.
2+
.
y2-y1
  
.
2，所以A、B兩點間的距離公式為AB=
(x2-x1)2+(y2-y1)2
．
注：上述公式對A、B在平面直角坐標系中其它位置也成立．
解答下列問題：
如圖2，直線l：y=2x+2與拋物線y=2x2交于A、B兩點，P為AB的中點，過P作x軸的垂線交拋物線于點C．
（1）求A、B兩點的坐標及C點的坐標；
（2）連結AB、AC，求證△ABC為直角三角形；
（3）將直線l平移到C點時得到直線l′，求兩直線l與l′的距離．

查看答案和解析>>

科目：初中數學 來源： 題型：

閱讀材料：如圖，AB=AC，BD=CD，則可證得AD平分∠BAC，據此我們引出了“角平分線”的尺規作法．

問題：如圖，AD=AE，AB=AC，也可證得AP平分∠BAC，據此我們能否引出了“角平分線”的第二種尺規作法呢？請在圖中嘗試著畫出∠α的平分線．

查看答案和解析>>

科目：初中數學 來源： 題型：閱讀理解

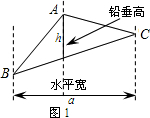閱讀材料：

如圖1，AB、CD交于點O，我們把△AOD和△BOC叫做對頂三角形．
結論：若△AOD和△BOC是對頂三角形，則∠A+∠D=∠B+∠C．
結論應用舉例：
如圖2：求五角星的五個內角之和，即∠A+∠B+∠ACE+∠ADB+∠E的度數．
解：連接CD，由對頂三角形的性質得：∠B+∠E=∠1+∠2，
在△ACD中，∵∠A+∠ACD+∠ADC=180°，
即∠A+∠3+∠1+∠2+∠4=180°，
∴∠A+∠ACE+∠B+∠E+ADB=180°
即五角星的五個內角之和為180°．
解決問題：
（1）如圖①，∠A+∠B+∠C+∠D+∠E+∠F=
360°
360°
；
（2）如圖②，∠A+∠B+∠C+∠D+∠E+∠F+∠G=
540°
540°
；
（3）如圖③，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
720°
720°
；
（4）如圖④，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=
1080°
1080°
；
請你從圖③或圖④中任選一個，寫出你的計算過程．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 在线观看不卡一区 | 在线播放国产一区二区三区 | 欧洲精品乱码久久久久蜜桃 | 欧日韩不卡在线视频 | 久久国产亚洲精品 | 男人天堂视频网 | 五月婷婷在线视频观看 | 久久国产美女 | 欧美日韩一区精品 | 亚洲精品久久久久久一区二区 | 色婷婷亚洲国产女人的天堂 | 久草在线在线精品观看 | 日韩在线视频观看 | av在线播放网站 | 国产美女精品人人做人人爽 | 久久福利 | 久久精品免费 | 一区二区三区影院 | 日韩精品一区二区在线 | 久久精品免费观看 | 日韩性视频 | 亚洲欧美综合精品久久成人 | 久久婷婷视频 | 99综合 | 日本一区二区三区四区视频 | 成年人福利 | 欧美一区二区成人 | 欧美激情网站 | 免费v片| 国产成人精品一区二区三区四区 | 欧洲一级毛片 | 国产精品国产自产拍高清 | 欧洲一区二区视频 | 欧美在线一区二区 | 国产免费拔擦拔擦8x高清在线人 | 国产激情在线 | 欧美精品欧美精品系列 | 欧美在线操 | 欧美 日韩 中文 | 久久国产精品精品国产 | 国产成人亚洲综合 |