解:(1)∵圓O的半徑為1,k=1時正方形的邊長為π+2,
∴當圓O從開始到與BC邊相切時,圓心O走過的路程為π+2-2=π;
當圓O從與AB邊相切到與DC邊相切時,圓心O走過的路程為2π;
當圓O與BC相切到與AD邊相切時,圓心O走過的路程為π;
當圓O從與DC邊相切到與AB邊相切時,圓心O走過的路程為2π,
∴圓心O走過的總路程為6π,又圓的周長為2π,
∴當k=1時,⊙O從開始滾動到停止,共滾動了3圈;
∵圓O的半徑為1,k=2時正方形的邊長為2π+2,
∴當圓O從開始到與BC邊相切時,圓心O走過的路程為2π;
當圓O從與AB邊相切到與DC邊相切時,圓心O走過的路程為3π;
當圓O與BC相切到與AD邊相切時,圓心O走過的路程為2π;
當圓O從與DC邊相切到與AB邊相切時,圓心O走過的路程為3π,
∴圓心O走過的總路程為10π,
又圓的周長為2π,
∴當k=2時,⊙O從開始滾動到停止,共滾動5圈;
同理:當k=n時,⊙O從開始滾動到停止,共滾動(2n+1)圈.
故答案為:3,5,2n+1;
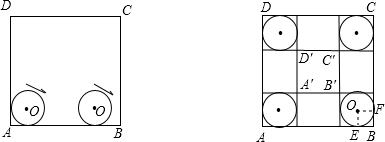
(2)如圖,連接OE,OF,
∵S
四邊形ABCD-S
四邊形A'B'C'D′=(nπ+2)
2-(nπ-2)
2
=[(nπ+2)+(nπ-2)][(nπ+2)-(nπ-2)]
=2nπ×4
=8nπ,
且S
圖形EFB=S
正方形OEBF-S
扇形OEF=1
2-
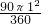
=1-

,
則⊙O滾過的面積S=S
四邊形ABCD-S
四邊形A'B'C'D′-4S
圖形EFB=8nπ-4(1-

)=8nπ+π-4.
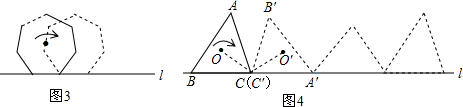
分析:(1)當k=1時,得出正方形的邊長為π+2,然后當圓O在邊AB上運動時,圓心O運動的路程為正方形的邊長減去圓的直徑;當圓O在BC邊上運動時,圓心O運動的路程為2π;當圓O在CD邊上運動時,同理圓心O的路程為π;當圓O在AD邊邊上運動時,圓心O運動的路程為2π,計算出總路程,除以圓的周長可得出圓轉動的圈數;當k=2時,得出正方形的邊長為2π+2,然后當圓O在邊AB上運動時,圓心O運動的路程為正方形的邊長減去圓的直徑,即為2π;當圓O在BC邊上運動時,圓心O運動的路程為3π;當圓O在CD邊上運動時,同理圓心O的路程為2π;當圓O在AD邊邊上運動時,圓心O運動的路程為3π,計算出總路程,除以圓的周長可得出圓轉動的圈數;同理當n=k時,歸納得到圓運動的圈數為2n+1;
(2)如圖,連接OE,OF,可得出四邊形OEBF為邊長為1的正方形,用正方形的面積減去扇形OEF的面積,可得出不規則圖形BEF的面積,然后由大正方形ABCD的面積-小正方形A′B′C′D′的面積-4圖形BEF的面積,可得出圓O滾過的面積.
點評:此題考查了切線的性質,正方形的性質,扇形面積公式,鍛煉了學生歸納總結,靈活轉化的能力,是一道綜合性較強的試題,要求學生掌握知識要全面.其中不規則圖形面積可以用規則圖形相加減來求,也可以通過平移,旋轉,拼割等方法來求.



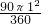 =1-
=1- ,
, )=8nπ+π-4.
)=8nπ+π-4.

 輕松奪冠全能掌控卷系列答案
輕松奪冠全能掌控卷系列答案