
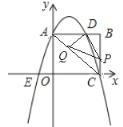
【題目】如圖,矩形![]() 中,
中,![]() 為原點,點
為原點,點![]() 在
在![]() 軸上,點
軸上,點![]() 在
在![]() 軸上,點
軸上,點![]() 的坐標為(4,3),拋物線
的坐標為(4,3),拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,與直線
,與直線![]() 交于點
交于點![]() ,與
,與![]() 軸交于
軸交于![]() 兩點.
兩點.
(1)求拋物線的表達式;
(2)點![]() 從點
從點![]() 出發,在線段
出發,在線段![]() 上以每秒1個單位長度的速度向點
上以每秒1個單位長度的速度向點![]() 運動,與此同時,點
運動,與此同時,點![]() 從點
從點![]() 出發,在線段
出發,在線段![]() 上以每秒
上以每秒![]() 個單位長度的速度向點
個單位長度的速度向點![]() 運動,當其中一點到達終點時,另一點也停止運動.連接
運動,當其中一點到達終點時,另一點也停止運動.連接![]() ,設運動時間為
,設運動時間為![]() (秒).
(秒).
①當![]() 為何值時,
為何值時,![]() 得面積最小?
得面積最小?
②是否存在某一時刻![]() ,使
,使![]() 為直角三角形?若存在,直接寫出
為直角三角形?若存在,直接寫出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
【答案】(1)![]() ;(2)①
;(2)① ![]() ;②
;②![]()
【解析】
(1)根據點B的坐標可得出點A,C的坐標,代入拋物線解析式即可求出b,c的值,求得拋物線的解析式;
(2)①過點Q、P作QF⊥AB、PG⊥AC,垂足分別為F、G,推出△QFA∽△CBA,△CGP∽△CBA,用含t的式子表示OF,PG,將三角形的面積用含t的式子表示出來,結合二次函數的性質可求出最值;②由于三角形直角的位置不確定,需分情況討論,根據點的坐標,再結合兩點間的距離公式用勾股定理求解即可.
解:(1)由題意知:A(0,3),C(4,0),
∵拋物線經過A、B兩點,
∴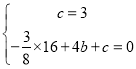 ,解得,
,解得,![]() ,
,
∴拋物線的表達式為:![]() .
.
(2)① ∵四邊形ABCD是矩形,
∴∠B=90O, ∴AC2=AB2+BC2=5;
由![]() ,可得
,可得![]() ,∴D(2,3).
,∴D(2,3).
過點Q、P作QF⊥AB、PG⊥AC,垂足分別為F、G,
∵∠FAQ=∠BAC, ∠QFA=∠CBA,
∴△QFA∽△CBA.
∴![]() ,
,
∴![]() .
.
同理:△CGP∽△CBA,
∴![]() ∴
∴![]() ,∴
,∴![]() ,
,
![]()
![]()
當![]() 時,△DPQ的面積最小.最小值為
時,△DPQ的面積最小.最小值為![]() .
.
② 由圖像可知點D的坐標為(2,3),AC=5,直線AC的解析式為:![]() .
.
三角形直角的位置不確定,需分情況討論:
當![]() 時,根據勾股定理可得出:
時,根據勾股定理可得出:
![]() ,
,
整理,解方程即可得解;
當![]() 時,可知點G運動到點B的位置,點P運動到C的位置,所需時間為t=3;
時,可知點G運動到點B的位置,點P運動到C的位置,所需時間為t=3;
當![]() 時,同理用勾股定理得出:
時,同理用勾股定理得出:
![]() ;
;
整理求解可得t的值.
由此可得出t的值為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.


 課課優能力培優100分系列答案
課課優能力培優100分系列答案 優百分課時互動系列答案
優百分課時互動系列答案科目:初中數學 來源: 題型:
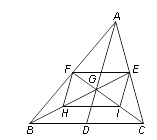
【題目】如圖,△ABC的中線AD、BE、CF相交于點G,H、I分別是BG、CG的中點.
(1)求證:四邊形EFHI是平行四邊形;
(2)①當AD與BC滿足條件 時,四邊形EFHI是矩形;
②當AD與BC滿足條件 時,四邊形EFHI是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,BD為一條對角線,AD∥BC,AD=2BC,∠ABD=90°,E為AD的中點,連接BE.
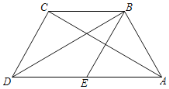
(1)求證:四邊形BCDE為菱形;
(2)連接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
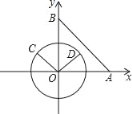
【題目】如圖,在平面直角坐標系中,已知點A(4,0),點B(0,4),動點C在以半徑為2的⊙O上,連接OC,過O點作OD⊥OC,OD與⊙O相交于點D,連接AB.
(1)若點C在第二象限的⊙O上運動,當OC∥AB時,∠BOC的度數為 ;
(2)若點C在整個⊙O上運動,當點C運動到什么位置時,△ABC的面積最大?并求出△ABC的面積的最大值;
(3)若點C在第一、二象限的⊙O上運動,連接AD,當OC∥AD時,
①求出點C的坐標;
②直線BC是否為⊙O的切線?請作出判斷,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
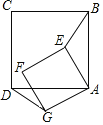
【題目】正方形ABCD和正方形AEFG,AB=12,AE=6![]() .設∠BAE=α(0°≤α≤45°,點E在正方形ABCD內部),BE的延長線交直線DG于點Q.
.設∠BAE=α(0°≤α≤45°,點E在正方形ABCD內部),BE的延長線交直線DG于點Q.
(1)求證:△ADG≌△ABE;
(2)試求出當α由0°變化到45°過程中,點Q運動的路線長,并畫出點Q的運動路徑;直接寫出當α等于多少度時,點G恰好在點Q運動的路徑上.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是測量一物體體積的過程:
步驟一:將180 mL的水裝進一個容量為300 mL的杯子中;
步驟二:將三個相同的玻璃球放入水中,結果水沒有滿;
步驟三:再將一個同樣的玻璃球放入水中,結果水滿溢出.

根據以上過程,推測一個玻璃球的體積在下列哪一范圍內?(1 mL=1 cm3)( ).
A. 10 cm3以上,20 cm3以下 B. 20 cm3以上,30 cm3以下
C. 30 cm3以上,40 cm3以下 D. 40 cm3以上,50 cm3以下
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(定義)函數圖象上的任意一點P(x,y),y﹣x稱為該點的“坐標差”,函數圖象上所有點的“坐標差”的最大值稱為該函數的“特征值”
(感悟)根據你的閱讀理解回答問題:
(1)點P (2,1)的“坐標差”為 ;(直接寫出答案)
(2)求一次函數y=2x+1(﹣2≤x≤3)的“特征值”;
(應用)(3)二次函數y=﹣x2+bx+c(bc≠0)交x軸于點A,交y軸于點B,點A與點B的“坐標差”相等,若此二次函數的“特征值”為﹣1,當m≤x≤m+3時,此函數的最大值為﹣2m,求m.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com