
【題目】如圖,四邊形ABCD是正方形,E是CD上的一點,△ABF是△ADE的旋轉圖形.
(1)寫成由△ADE順時針旋轉到△ABF的旋轉中心、旋轉角的度數.
(2)連接EF,判斷并說明△AEF的形狀.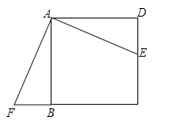
【答案】解: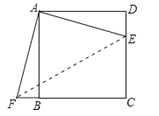
(1)∵△ABF是△ADE的旋轉圖形,
∴旋轉中心是點A;
∵順時針旋轉了90,
∴旋轉角的度數90;
(2)△AEF的形狀是等腰直角三角形,理由如下:
∵△ABF是△ADE的旋轉圖形,旋轉角為90°,
∴AE=AF,∠FAE=90°,
∴△AEF是等腰直角三角形.
【解析】(1)利用旋轉的性質得出旋轉中心即可;利用旋轉的位置得出旋轉角即可;
(2)利用旋轉的性質以及等腰三角形的判定得出即可.
【考點精析】根據題目的已知條件,利用旋轉的性質的相關知識可以得到問題的答案,需要掌握①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】已知在△ABC中,AB=AC=5,BC=6,AD是BC邊上的中線,四邊形ADBE是平行四邊形.
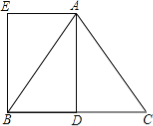
(1)求證:四邊形ADBE是矩形;
(2)求矩形ADBE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知Rt△ABC中,∠C=90°,AC=8.BC=6,點P以每秒1個單位的速度從
A向C運動,同時點Q以每秒2個單位的速度從A→B→C方向運動,它們到C點后都
停止運動,設點P、Q運動的時間為t秒.
(Ⅰ)在運動過程中,請你用t表示P、Q兩點間的距離,并求出P、Q兩點間的距離
的最大值;
(Ⅱ)經過t秒的運動,求△ABC被直線PQ掃過的面積S與時間t的函數關系式.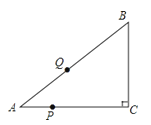
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列結論:
①若a+b+c=0,且abc≠0,則![]() ;
;
②若a+b+c=0,且a≠0,則x=1一定是方程ax+b+c=0的解;
③若a+b+c=0,且abc≠0,則abc>0;
④若|a|>|b|,則![]() >0.
>0.
其中正確的結論是( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
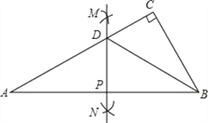
【題目】如圖,△ABC中,∠C=90°,∠A=30°.分別以頂點A,B為圓心,大于![]() AB的長為半徑作弧,兩弧在直線AB兩側分別交于M,N兩點,過M,N作直線交AB于點P,交AC于點D,連結BD.下列結論中,錯誤的是( )
AB的長為半徑作弧,兩弧在直線AB兩側分別交于M,N兩點,過M,N作直線交AB于點P,交AC于點D,連結BD.下列結論中,錯誤的是( )
A. 直線AB是線段MN的垂直平分線 B. CD=![]() AD
AD
C. BD平分∠ABC D. S△APD=S△BCD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如今,網上購物已成為一種新的消費時尚,精品書店想購買一種賀年卡在元旦時銷售,在互聯網上搜索了甲、乙兩家網
店(如圖所示),已知兩家網店的這種賀年卡的質量相同,請看圖回答下列問題:
(1)假若精品書店想購買x張賀年卡,那么在甲、乙兩家網店分別需要花多少錢(用含有x的式子表示)?(提示:如需付運費時運費只需付一次,即8元)
(2)精品書店打算購買300張賀年卡,選擇哪家網店更省錢?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠BOC=9°,點A在OB上,且OA=1,按下列要求畫圖:
以A為圓心,1為半徑向右畫弧交OC于點A1,得第1條線段AA1;再以A1為圓心,1為半徑向右畫弧交OB于點A2,得第2條線段A1A2;再以A2為圓心,1為半徑向右畫弧交OC于點A3,得第3條線段A2A3;…這樣畫下去,直到得第n條線段,之后就不能再畫出符合要求的線段了,則n=______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年以來,國務院連續發布了《關于加快構建大眾創業萬眾創新支撐平臺的指導意見》等一系列支持性政策,各地政府高度重視、積極響應,中國掀起了大眾創業萬眾創新的新浪潮.某創新公司生產營銷A、B兩種新產品,根據市場調研,發現如下信息:
信息1:銷售A種產品所獲利潤y(萬元)與所售產品x(噸)之間存在二次函數關系y=ax2+bx,當x=1時,y=7;當x=2時,y=12.
信息2:銷售B種產品所獲利潤y(萬元)與所售產品x(噸)之間存在正比例函數關系y=2x.
根據以上信息,解答下列問題:
(1)求a,b的值;
(2)該公司準備生產營銷A、B兩種產品共10噸,請設計一個生產方案,使銷售A、B兩種產品獲得的利潤之和最大,最大利潤是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com