
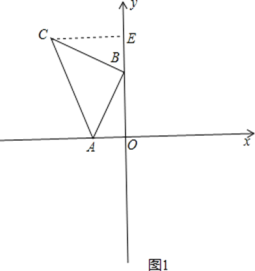
【題目】如圖 1,A(-2,0),B(0,4),以 B 點為直角頂點在第二象限作等腰直角△ABC.

(1)求 C 點的坐標;
(2)在坐標平面內是否存在一點 P,使△PAB 與△ABC 全等?若存在,直接寫出 P 點坐標,若不存在,請說明理由;
(3)如圖 2,點 E 為 y 軸正半軸上一動點, 以 E 為直角頂點作等腰直角△AEM,過 M 作 MN⊥x 軸于 N,求 OE-MN 的值.
【答案】(1)C(-4,6);(2)存在一點P,使△PAB與△ABC全等,符合條件的P的坐標是(-6,2)或(2,-2)或(4,2)或(-4,6);(3)2.
【解析】
(1))作CE⊥y軸于E,證△CEB≌△BOA,推出CE=OB=4,BE=AO=2,即可得出答案;
(2)分為四種情況,畫出符合條件的圖形,構造直角三角形,證三角形全等,即可得出答案;
(3)作MF⊥y軸于F,證△EFM≌△AOE,求出EF,即可得出答案.
解:(1)作CE⊥y軸于E,如圖1,
∵A(-2,0),B(0,4),
∴OA=2,OB=4,
∵∠CBA=90°,
∴∠CEB=∠AOB=∠CBA=90°,
∴∠ECB+∠EBC=90°,∠CBE+∠ABO=90°,
∴∠ECB=∠ABO,
在△CBE和△BAO中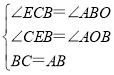
∴△CBE≌△BAO,
∴CE=BO=4,BE=AO=2,
即OE=2+4=6,
∴C(-4,6).
(2)存在一點P,使△PAB與△ABC全等,
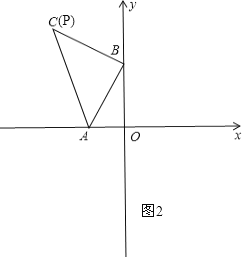
分為四種情況:①如圖2,當P和C重合時,△PAB和△ABC全等,即此時P的坐標是(-4,6);
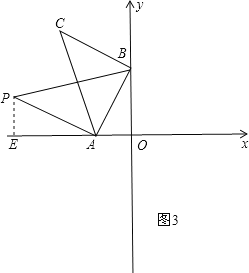
②如圖3,過P作PE⊥x軸于E,
則∠PAB=∠AOB=∠PEA=90°,
∴∠EPA+∠PAE=90°,∠PAE+∠BAO=90°,
∴∠EPA=∠BAO,
在△PEA和△AOB中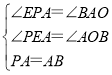
∴△PEA≌△AOB,
∴PE=AO=2,EA=BO=4,
∴OE=2+4=6,
即P的坐標是(-6,2);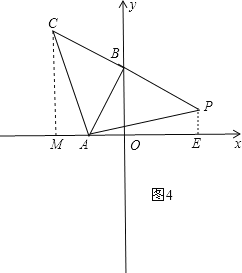
③如圖4,過C作CM⊥x軸于M,過P作PE⊥x軸于E,
則∠CMA=∠PEA=90°,
∵△CBA≌△PBA,
∴∠PAB=∠CAB=45°,AC=AP,
∴∠CAP=90°,
∴∠MCA+∠CAM=90°,∠CAM+∠PAE=90°,
∴∠MCA=∠PAE,
在△CMA和△AEP中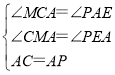
∴△CMA≌△AEP,
∴PE=AM,CM=AE,
∵C(-4,6),A(-2,0),
∴PE=4-2=2,OE=AE-A0=6-2=4,
即P的坐標是(4,2);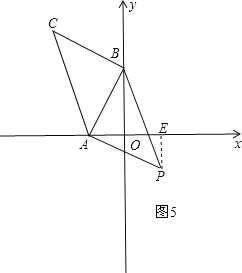
④如圖5,過P作PE⊥x軸于E,
∵△CBA≌△PAB,
∴AB=AP,∠CBA=∠BAP=90°,
則∠AEP=∠AOB=90°,
∴∠BAO+∠PAE=90°,∠PAE+∠APE=90°,
∴∠BAO=∠APE,
在△AOB和△PEA中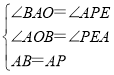
∴△AOB≌△PEA,
∴PE=AO=2,AE=OB=4,
∴0E=AE-AO=4-2=2,
即P的坐標是(2,-2),
綜合上述:符合條件的P的坐標是(-6,2)或(2,-2)或(4,2)或(-4,6).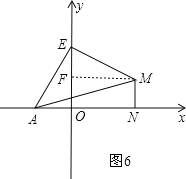
(3)如圖6,作MF⊥y軸于F,
則∠AEM=∠EFM=∠AOE=90°,
∵∠AEO+∠MEF=90°,∠MEF+∠EMF=90°,
∴∠AEO=∠EMF,
在△AOE和△EMF中
∵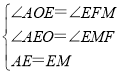
∴△AEO≌△EMF(AAS),
∴EF=AO=2,MF=OE,
∵MN⊥x軸,MF⊥y軸,
∴∠MFO=∠FON=∠MNO=90°,
∴四邊形FONM是矩形,
∴MN=OF,
∴OE-MN=OE-OF=EF=OA=2.
故答案為:(1)C(-4,6);(2)存在一點P,使△PAB與△ABC全等,符合條件的P的坐標是(-6,2)或(2,-2)或(4,2)或(-4,6);(3)2.


 考前必練系列答案
考前必練系列答案科目:初中數學 來源: 題型:
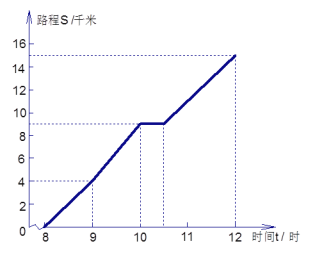
【題目】圖為一位旅行者在早晨8時從城市出發到郊外所走的路程S(單位:千米)與時間t(單位:時)的變量關系的圖象.根據圖象回答問題:
(1)在這個變化過程中,自變量是________,因變量是________.
(2)9時,10時,所走的路程分別是多少?
(3)他休息了多長時間?
(4)他從休息后直至到達目的地這段時間的平均速度是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 與
與![]() 的平分線交于點
的平分線交于點![]() ,求證:
,求證:![]() 是等腰三角形.
是等腰三角形.
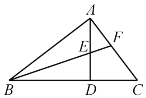
(2).閱讀下列文字:我們知道,對于一個圖形,通過兩種不同的方法計算它的面積,可以得到一個數學等式.例如由圖1可以得到 ![]() .請解答下列問題:
.請解答下列問題:
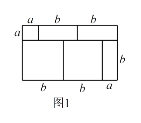
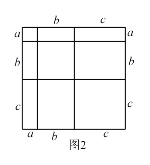
①.寫出圖2中所表示的數學等式;
②.利用(1)中所得到的結論,解決下面的問題:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:初中數學 來源: 題型:
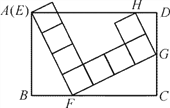
【題目】如圖,由8個大小相等的小正方形構成的圖案,它的四個頂點 E,F,G,H分別在矩形ABCD的邊AB,BC,CD,DA上,若AB=4,BC=6,則DG的長是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
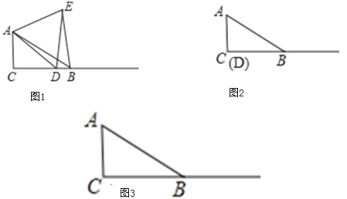
【題目】問題:如圖1,在Rt△ABC中,∠C=90°,∠ABC=30°,點D是邊CB上任意一點,△ADE是等邊三角形,且點E在∠ACB的內部,連接BE.探究線段BE與DE之間的數量關系.請你完成下列探究過程:先將圖形特殊化,得出猜想,再對一般情況進行分析并加以證明.
(1)當點D與點C重合時(如圖2),請你補全圖形.由∠BAC的度數為 ,點E落在 ______ ,容易得出BE與DE之間的數量關為 ;
(2)當點D是BC上任意一點(不與點B、C重合)時,結合圖1,探究(1)中線段BE與DE之間的數量關系是否還成立?并證明你的結論.
(3)如圖3,若點P為直線BC上一點,若△PAB為等腰三角形,請你求出∠APB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
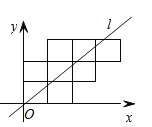
【題目】八個邊長為1的正方形如圖擺放在平面直角坐標系中,經過原點的一條直線![]() 將這八個正方形分成面積相等的兩部分,則該直線
將這八個正方形分成面積相等的兩部分,則該直線![]() 的解析式為( )
的解析式為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某村在推進美麗鄉村活動中,決定建設幸福廣場,計劃鋪設相同大小規格的紅色和藍色地磚.經過調査.獲取信息如下:
購買數量低于5000塊 | 購買數量不低于5000塊 | |
紅色地磚 | 原價銷售 | 以八折銷售 |
藍色地磚 | 原價銷售 | 以九折銷售 |
如果購買紅色地磚4000塊,藍色地磚6000塊,需付款86000元;如果購買紅色地磚10000塊,藍色地磚3500塊,需付款99000元.
(1)紅色地磚與藍色地磚的單價各多少元?
(2)經過測算,需要購置地磚12000塊,其中藍色地磚的數量不少于紅色地磚的一半,并且不超過6000塊,如何購買付款最少?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在東營市中小學標準化建設工程中,某學校計劃購進一批電腦和電子白板,經過市場考察得知,購買1臺電腦和2臺電子白板需要3.5萬元,購買2臺電腦和1臺電子白板需要2.5萬元.
(1)求每臺電腦、每臺電子白板各多少萬元?
(2)根據學校實際,需購進電腦和電子白板共30臺,總費用不超過30萬元,但不低于28萬元,請你通過計算求出有幾種購買方案,哪種方案費用最低.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com