
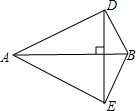
 如圖,已知:四邊形AEBD中,對角線AB和DE相交于點C,且AB垂直平分DE,AC=a,BC=b,CD=
如圖,已知:四邊形AEBD中,對角線AB和DE相交于點C,且AB垂直平分DE,AC=a,BC=b,CD= ,其中a≥b>0.
,其中a≥b>0. 的大小關系,并利用圖形中線段的數量關系證明你的結論.
的大小關系,并利用圖形中線段的數量關系證明你的結論. 解:(1)如圖所示
解:(1)如圖所示 ,
,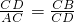
 ;
; ,
, .
. ,因此可得出:a+b≥2
,因此可得出:a+b≥2 .
.

 階梯計算系列答案
階梯計算系列答案科目:初中數學 來源: 題型:
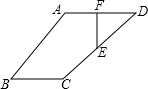 如圖,已知在四邊形ABCD中,E、F分別為AD、DC的中點,AD∥BC,AD:DC=1:
如圖,已知在四邊形ABCD中,E、F分別為AD、DC的中點,AD∥BC,AD:DC=1:| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知平行四邊形ABOC的頂點A、B、C在二次函數y=ax2+bx+c的圖象上,又點A、B分別在y軸和x軸上,∠ABO=45°.圖象頂點的橫坐標為2,求二次函數解析式.
如圖,已知平行四邊形ABOC的頂點A、B、C在二次函數y=ax2+bx+c的圖象上,又點A、B分別在y軸和x軸上,∠ABO=45°.圖象頂點的橫坐標為2,求二次函數解析式.查看答案和解析>>
科目:初中數學 來源: 題型:
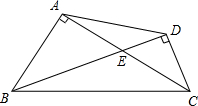 (2013•奉賢區一模)如圖,已知在四邊形ABCD中,AC⊥AB,BD⊥CD,AC與BD相交于點E,S△AED=9,S△BEC=25.
(2013•奉賢區一模)如圖,已知在四邊形ABCD中,AC⊥AB,BD⊥CD,AC與BD相交于點E,S△AED=9,S△BEC=25.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com