
 在平面直角坐標系xOy中,反比例函數y=$\frac{k}{x}$(k≠0)的圖象過(2,3).
在平面直角坐標系xOy中,反比例函數y=$\frac{k}{x}$(k≠0)的圖象過(2,3).分析 (1)把點(2,3)代入反比例函數求出k的值即可;
(2)分兩種情況,分別求出AM與OM的關系,即可得出m的值.
解答 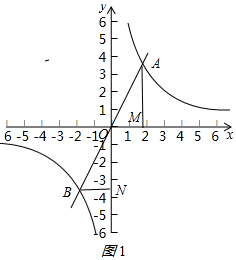 解:(1)∵反比例函數$y=\frac{k}{x}$(k≠0)的圖象過(2,3),
解:(1)∵反比例函數$y=\frac{k}{x}$(k≠0)的圖象過(2,3),
∴$3=\frac{k}{2}$,
解得k=6,
∴反比例函數表達式為$y=\frac{6}{x}$
(2)分兩種情況:
①如圖1所示:AM=2BN,
由對稱的性質得:點A和B關于原點O對稱,
則OA=OB,OM=BN,
∴AM=2OM,
∴m=2;
②如圖2所示:BN=2AM,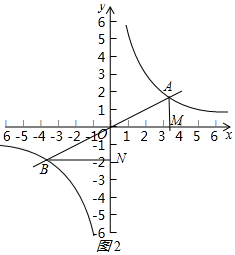
由對稱的性質得:點A和B關于原點O對稱,
則OA=OB,OM=BN,
∴AM=2OM,
∴m=$\frac{1}{2}$
∴m=2或m=$\frac{1}{2}$.
點評 本題考查了反比例函數與一次函數的交點問題,待定系數法求反比例函數與一次函數的解析式,也考查了觀察函數圖象的能力.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 若平面直角坐標系中的點作如下平移:沿x軸方向平移的數量為a(向右為正,向左為負,平移|a|個單位),沿y軸方向平移的數量為b(向上為正,向下為負,平移|b|個單位),則把有序數對{a,b}叫做這一平移的“平移量”.規定“平移量”{a,b}與“平移量”{c,d}的加法運算法則為{a,b}+{c,d}={a+c,b+d}.
若平面直角坐標系中的點作如下平移:沿x軸方向平移的數量為a(向右為正,向左為負,平移|a|個單位),沿y軸方向平移的數量為b(向上為正,向下為負,平移|b|個單位),則把有序數對{a,b}叫做這一平移的“平移量”.規定“平移量”{a,b}與“平移量”{c,d}的加法運算法則為{a,b}+{c,d}={a+c,b+d}.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
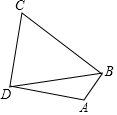 已知:在四邊形ABCD中,∠ABC=90°,∠C=60,AB=$\frac{\sqrt{3}}{2}$,BC=1+$\sqrt{3}$,CD=2
已知:在四邊形ABCD中,∠ABC=90°,∠C=60,AB=$\frac{\sqrt{3}}{2}$,BC=1+$\sqrt{3}$,CD=2查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
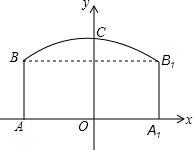 如圖,隧道的截面由拋物線和長方形構成.長方形的長為12m,寬為5m,拋物線的最高點C離路面AA1的距離為8m,建立如圖所示的直角坐標系.
如圖,隧道的截面由拋物線和長方形構成.長方形的長為12m,寬為5m,拋物線的最高點C離路面AA1的距離為8m,建立如圖所示的直角坐標系.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com