
設關于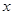 的方程
的方程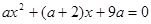 ,有兩個不相等的實數根
,有兩個不相等的實數根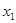 、
、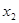 ,且
,且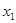
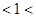
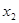 ,那么實數
,那么實數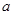 的取值范圍是 ( )
的取值范圍是 ( )
A.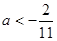 | B.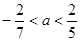 | C.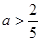 | D.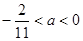 |
D
解析考點:根與系數的關系;根的判別式.
專題:轉化思想.
分析:根據一元二次方程的根的判別式,建立關于a的不等式,求出a的取值范圍.又存在x1<1<x2,即(x1-1)(x2-1)<0,
x1x2-(x1+x2)+1<0,利用根與系數的關系,從而最后確定a的取值范圍.
解答:解:∵方程有兩個不相等的實數根,
則△>0,
∴(a+2)2-4a×9a=-35a2+4a+4>0,
解得- <a<
<a<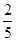 ,
,
∵x1+x2=-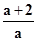 ,x1x2=9,
,x1x2=9,
又∵x1<1<x2,
∴x1-1<0,x2-1>0,
那么(x1-1)(x2-1)<0,
∴x1x2-(x1+x2)+1<0,
即9+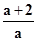 +1<0,
+1<0,
解得-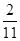 <a<0,
<a<0,
最后a的取值范圍為:-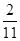 <a<0.
<a<0.
故選D.
點評:總結:1、一元二次方程根的情況與判別式△的關系:
(1)△>0?方程有兩個不相等的實數根;
(2)△=0?方程有兩個相等的實數根;
(3)△<0?方程沒有實數根.
2、根與系數的關系為:x1+x2="-" 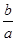 ,x1x2=
,x1x2= 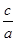
.


科目:初中數學 來源:2010年湖北省某市新人教版中考數學模擬試卷(6)(解析版) 題型:解答題
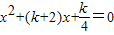 有兩個不相等的實數根.
有兩個不相等的實數根.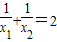 成立?若存在,請求出k的值;若不存在,請說明理由.
成立?若存在,請求出k的值;若不存在,請說明理由.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com