
【題目】如圖,△ABC中,∠A=30°,∠B=70°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,求∠CDF的度數.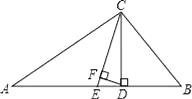
【答案】解:∵∠A=30°,∠B=70°,
∴∠ACB=180°﹣∠A﹣∠B=80°.
∵CE平分∠ACB,
∴∠ACE= ![]() ∠ACB=40°.
∠ACB=40°.
∵CD⊥AB于D,
∴∠CDA=90°,
∠ACD=180°﹣∠A﹣∠CDA=60°.
∴∠ECD=∠ACD﹣∠ACE=20°.
∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF=180°﹣∠CFD﹣∠ECD=70°
【解析】首先根據三角形的內角和定理求得∠ACB的度數,以及∠BCD的度數,根據角的平分線的定義求得∠BCE的度數,則∠ECD可以求解,然后在△CDF中,利用內角和定理即可求得∠CDF的度數.
【考點精析】本題主要考查了三角形的內角和外角的相關知識點,需要掌握三角形的三個內角中,只可能有一個內角是直角或鈍角;直角三角形的兩個銳角互余;三角形的一個外角等于和它不相鄰的兩個內角的和;三角形的一個外角大于任何一個和它不相鄰的內角才能正確解答此題.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC, ∠ABC、∠ACB的三等分線交于點E、D,若∠BFC=132°,∠BGC=118°,則∠A的度數為( )
A.65°
B.66°
C.70°
D.78°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】實驗探究:
(1)動手操作:
①如圖1,將一塊直角三角板DEF放置在直角三角板ABC上,使三角板DEF的兩條直角邊DE、DF分別經過點B、C,且BC∥EF,已知∠A=30°,則∠ABD+∠ACD=;
②如圖2,若直角三角板ABC不動,改變等腰直角三角板DEF的位置,使三角板DEF的兩條直角邊DE、DF仍然分別經過點B、C,那么∠ABD+∠ACD= 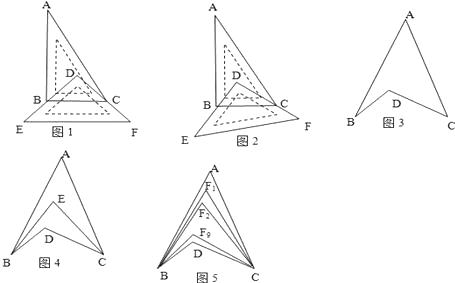
(2)猜想證明:
如圖3,∠BDC與∠A、∠B、∠C之間存在著什么關系,并說明理由;
(3)靈活應用:
請你直接利用以上結論,解決以下列問題:
①如圖4,BE平分∠ABD,CE平分∠ACB,若∠BAC=40°,∠BDC=120°,求∠BEC的度數;
(4)②如圖5,∠ABD,∠ACD的10等分線相交于點F1、F2、…、F9 ,
若∠BDC=120°,∠BF3C=64°,則∠A的度數為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過矩形ABCD的四個頂點作對角線AC、BD的平行線,分別相交于E、F、G、H四點,則四邊形EFGH為( )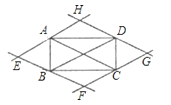
A.平行四邊形
B.矩形
C.菱形
D.正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,作AD⊥AB交BC的延長線于點D,作CE⊥AC,且使AE∥BD,連結DE.
(1)求證:AD=CE.
(2)若DE=3,CE=4,求tan∠DAE的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格中,每個小正方形的邊長均為1,每個小正方形的頂點稱為格點.請在給出的5×5的正方形網格中,以格點為頂點,畫出兩個三角形,一個三角形的長分別是 ![]() 、2、
、2、 ![]() ,另一個三角形的三邊長分別是
,另一個三角形的三邊長分別是 ![]() 、2
、2 ![]() 、5
、5 ![]() .(畫出的兩個三角形除頂點和邊可以重合外,其余部分不能重合)
.(畫出的兩個三角形除頂點和邊可以重合外,其余部分不能重合) 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com