

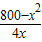 (0<x<20
(0<x<20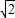 ).
). y2
y2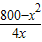 +80(
+80(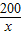 -
-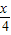 )2
)2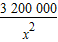 +76000(0<x<20
+76000(0<x<20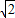 ).
).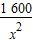 -80)+76000+2000×80=2000×(x-
-80)+76000+2000×80=2000×(x-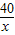 )2+236000>235000.
)2+236000>235000.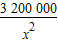 +76000=308000,
+76000=308000,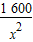 =0.
=0.

科目:初中數學 來源: 題型:
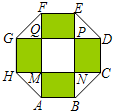
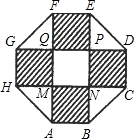 某住宅小區,為美化環境,提高居民生活質量,要建一個八邊形居民廣場(平面圖如圖,其中,正方形MNPQ與四個相同矩形(圖中陰影部分)的面積的和為800m2.
某住宅小區,為美化環境,提高居民生活質量,要建一個八邊形居民廣場(平面圖如圖,其中,正方形MNPQ與四個相同矩形(圖中陰影部分)的面積的和為800m2.查看答案和解析>>
科目:初中數學 來源: 題型:
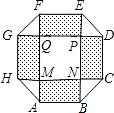 某住宅小區,為美化環境,提高居民的生活質量,想要建造一個八邊形的居民廣場,如圖,其中正方形MNPQ同長方形(圖中的陰影部分)的面積的和為a(a+4b),正方形MNPQ的邊長為a,則八邊形ABCDEFGH的面積為( )
某住宅小區,為美化環境,提高居民的生活質量,想要建造一個八邊形的居民廣場,如圖,其中正方形MNPQ同長方形(圖中的陰影部分)的面積的和為a(a+4b),正方形MNPQ的邊長為a,則八邊形ABCDEFGH的面積為( )| A、a2+4ab+2b2 | B、a2+4ab+4b2 | C、a2+8ab | D、a2+6ab+2b2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2004年全國中考數學試題匯編《二次函數》(03)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2004年云南省中考數學試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com