
如圖l,已知∠AOC=m°,∠BOC=n°且m、n滿足等式|3m-420|+(2n-40)2=0,射線OP從OB處繞點0以4度/秒的速度逆時針旋轉.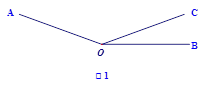
(1)試求∠AOB的度數;
(2)如圖l,當射線OP從OB處繞點O開始逆時針旋轉,同時射線OQ從OA處以l度/秒的速度繞點0順時針旋轉,當他們旋轉多少秒時,使得∠POQ=10°?
(3)如圖2,若射線OD為∠AOC的平分線,當射線OP從OB處繞點O開始逆時針旋轉,同時射線OT從射線OD處以x度/秒的速度繞點O順時針旋轉,使得這兩條射線重合于射線OE處(OE在∠DOC的內部)時,且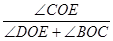 =
=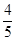 ,試求x.
,試求x.
(1)160°;(2)30秒或34秒;(3)2
解析試題分析:(1)先根據非負數的性質求得m=140,n=20,即得∠AOC=140°,∠BOC=20°,從而得到結果;
(2)設他們旋轉x秒時,使得∠POQ=10°,則∠AOQ=x°,∠BOP=4x°,分局①當射線OP與射線OQ相遇前,②當射線OP與射線OQ相遇后,兩種情況,結合旋轉的性質分析即可;
(3)設t秒后這兩條射線重合于射線OE處,則∠BOE=4t°,先根據角平分線的性質可得∠COD的度數,即可求得∠BOD的度數,再根據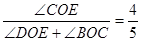 即可求得∠COE的度數,從而得到∠DOE、∠BOE的度數,即可求得結果.
即可求得∠COE的度數,從而得到∠DOE、∠BOE的度數,即可求得結果.
(1)∵|3m-420|+(2n-40)2=0
∴3m-420=0且2n-40=0
∴m=140,n=20
∴∠AOC=140°,∠BOC=20°
∴∠AOB=∠AOC+∠BOC=160°;
(2)設他們旋轉x秒時,使得∠POQ=10°,則∠AOQ=x°,∠BOP=4x°
①當射線OP與射線OQ相遇前有:∠AOQ+∠POQ+∠BOP+∠POQ =∠AOB=160°
即x+4x+10=160,解得x=30;
②當射線OP與射線OQ相遇后有:∠AOQ+∠POQ+∠BOP-∠POQ =∠AOB=160°
即x+4x-10=160,解得x=34
答:當他們旋轉30秒或34秒時,使得∠POQ=10°;
(3)設t秒后這兩條射線重合于射線OE處,則∠BOE=4t°
∵OD為∠AOC的平分線
∴∠COD= ∠AOC=70°
∠AOC=70°
∴∠BOD=∠COD+∠BOC=70°+20°=90°
∵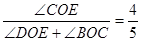
∴∠COE=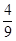 ×90°=40°
×90°=40°
∠DOE=30°,∠BOE=20°+40°=60°
即4t=60,t=15
∴∠DOE=15x°
即15x=30,x=2.
考點:旋轉的綜合題
點評:本題知識點較多,綜合性強,難度較大,需要學生熟練掌握旋轉的性質.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 ,0),過A,C,D的拋物線與(1)所得的四邊形OABC的邊BC交于點E,求拋物線的解析式及點E的坐標;
,0),過A,C,D的拋物線與(1)所得的四邊形OABC的邊BC交于點E,求拋物線的解析式及點E的坐標;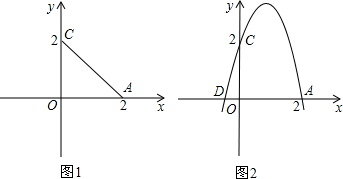
查看答案和解析>>
科目:初中數學 來源:2015屆湖北省武漢市青山區七年級第一學期期末測試數學試卷(解析版) 題型:解答題
如圖l,已知∠AOC=m°,∠BOC=n°且m、n滿足等式|3m-420|+(2n-40)2=0,射線OP從OB處繞點0以4度/秒的速度逆時針旋轉.
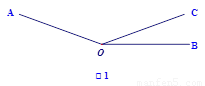
(1)試求∠AOB的度數;
(2)如圖l,當射線OP從OB處繞點O開始逆時針旋轉,同時射線OQ從OA處以l度/秒的速度繞點0順時針旋轉,當他們旋轉多少秒時,使得∠POQ=10°?
(3)如圖2,若射線OD為∠AOC的平分線,當射線OP從OB處繞點O開始逆時針旋轉,同時射線OT從射線OD處以x度/秒的速度繞點O順時針旋轉,使得這兩條射線重合于射線OE處(OE在∠DOC的內部)時,且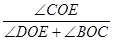 =
=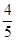 ,試求x.
,試求x.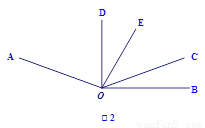
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com