
【題目】已知:如圖,AB為⊙O的直徑,AB⊥AC,BC交⊙O于D,E是AC的中點,ED與AB的延長線相交于點F.

(1)求證:DE為⊙O的切線.
(2)求證:AB:AC=BF:DF.
【答案】詳見解析
【解析】
(1)連接OD、AD,求出CDA=∠BDA=90°,求出∠1=∠4,∠2=∠3,推出∠4+∠3=∠1+∠2=90°,根據切線的判定推出即可;
(2)證△ABD∽△CAD,劉![]() ,證△FAD∽△FDB,得
,證△FAD∽△FDB,得![]() ,即可得出AB:AC=BF:DF。
,即可得出AB:AC=BF:DF。
證明:(1)連接DO、DA,
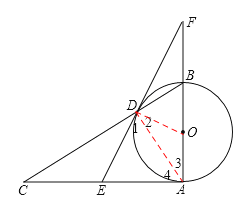
∵AB為⊙O直徑,∴∠CDA=∠BDA=90°。
∵CE=EA,∴DE=EA。∴∠1=∠4。
∵OD=OA,∴∠2=∠3。
∵∠4+∠3=90°,∴∠1+∠2=90°,即:∠EDO=90°。
∴DE⊥OD。
∵OD是半徑,∴DE為⊙O的切線。
(2)∵∠3+∠DBA=90°,∠3+∠4=90°,
∴∠4=∠DBA。
∵∠CDA=∠BDA=90°,∴△ABD∽△CAD。
∴![]() 。
。
∵∠FDB+∠BDO=90°,∠DBO+∠3=90°,
又∵OD=OB,∴∠BDO=∠DBO。∴∠3=∠FDB。
∵∠F=∠F,∴△FAD∽△FDB。∴![]() 。
。
∴![]() ,即AB:AC=BF:DF。
,即AB:AC=BF:DF。


 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,AD是高,BE是中線,CF是角平分線,CF交AD于G,交BE于H.下列結論:①S△ABE=S△BCE;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.其中所有正確結論的序號是
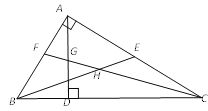
A.①②③④B.①②③C.②④D.①③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題正確的個數是
①若代數式![]() 有意義,則x的取值范圍為x≤1且x≠0.
有意義,則x的取值范圍為x≤1且x≠0.
②我市生態旅游初步形成規模,2012年全年生態旅游收入為302 600 000元,保留三個有效數字用科學記數法表示為3.03×108元.
③若反比例函數![]() (m為常數),當x>0時,y隨x增大而增大,則一次函數y=﹣2x+m的圖象一定不經過第一象限.
(m為常數),當x>0時,y隨x增大而增大,則一次函數y=﹣2x+m的圖象一定不經過第一象限.
④若函數的圖象關于y軸對稱,則函數稱為偶函數,下列三個函數:y=3,y=2x+1,y=x2中偶函數的個數為2個.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋里裝有分別標有漢字“靈”、“秀”、“鄂”、“州”的四個小球,除漢字不同之外,小球沒有任何區別,每次摸球前先攪拌均勻再摸球.
(1)若從中任取一個球,球上的漢字剛好是“鄂”的概率為多少?
(2)甲從中任取一球,不放回,再從中任取一球,請用樹狀圖的方法,求出甲取出的兩個球上的漢字恰能組成“靈秀”或“鄂州”的概率P1;
(3)乙從中任取一球,記下漢字后再放回袋中,然后再從中任取一球,記乙取出的兩個球上的漢字恰能組成“靈秀”或“鄂州”的概率為P2,指出P1,P2的大小關系(請直接寫出結論,不必證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中小正方形的邊長為1,△ABC的三個頂點都在小正方形的格點上,求:
(1)邊AC,AB,BC的長;
(2)點C到AB邊的距離;
(3)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,這個圖案是3世紀我國漢代數學家趙爽在注解《周髀算經》時給出的,人們稱它為“趙爽弦圖”.已知AE=3,BE=2,若向正方形ABCD內隨意投擲飛鏢(每次均落在正方形ABCD內,且落在正方形ABCD內任何一點的機會均等),則恰好落在正方形EFGH內的概率為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在濟南市開展的“美麗泉城,創衛我同行”活動中,某校倡議七年級學生利用雙休日在各自社區參加義務勞動.為了解同學們勞動情況,學校隨機調查了部分同學的勞動時間,并用得到的數據繪制成不完整的統計圖表,如圖所示:
勞動時間(時) | 頻數(人數) | 頻率 |
0.5 | 12 | 0.12 |
1 | 30 | 0.3 |
1.5 | x | 0.4 |
2 | 18 | y |
合計 | m | 1 |
(1)統計表中的x= ,y= ;
(2)被調查同學勞動時間的中位數是 時;
(3)請將頻數分布直方圖補充完整;
(4)求所有被調查同學的平均勞動時間.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,D是BC的中點,過D點的直線GF交AC于F,交AC的平行線BG于G點,DE⊥DF,交AB于點E,連結EG、EF.

(1)求證:BG=CF.
(2)請你判斷BE+CF與EF的大小關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com