
【題目】已知一次函數圖象經過A(-2,-3),B(1,3)兩點.
⑴ 求這個一次函數的解析式.
⑵ 試判斷點P(-1,1)是否在這個一次函數的圖象上.
⑶ 求此函數與x軸、y軸圍成的三角形的面積.
【答案】解:(1)設一次函數的表達式為y=kx+b,
則-3=-2k+b、3=k+b,解得:k=2,b=1.
∴函數的解析式為:y=2x+1。
(2)將點P(-1,1)代入函數解析式,1≠-2+1,
∴點P不在這個一次函數的圖象上。
(3)當x=0,y=1,當y=0,x=![]() ,
,
此函數與x軸、y軸圍成的三角形的面積為:![]() ×1×∣
×1×∣![]() ∣=
∣=![]() =0.25。
=0.25。
【解析】(1)用待定系數法求解函數解析式;
(2)將點P坐標代入即可判斷;
(3)求出函數與x軸、y軸的交點坐標,后根據三角形的面積公式即可求解.
【考點精析】掌握一次函數的性質和確定一次函數的表達式是解答本題的根本,需要知道一般地,一次函數y=kx+b有下列性質:(1)當k>0時,y隨x的增大而增大(2)當k<0時,y隨x的增大而減小;確定一個一次函數,需要確定一次函數定義式y=kx+b(k不等于0)中的常數k和b.解這類問題的一般方法是待定系數法.


科目:初中數學 來源: 題型:
【題目】下列命題中,①9的平方根是3;②9的平方根是±3;③﹣0.027沒有立方根;④﹣3是27的負的立方根;⑤一個數的平方根等于它的算術平方根,則這個數是0;⑥ ![]() 的平方根是±4,其中正確的有( )
的平方根是±4,其中正確的有( )
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了推動球類運動的普及,成立多個球類運動社團,為此,學生會采取抽樣調查的方法,從足球、乒乓球、籃球、排球四個項目調查了若干名學生的興趣愛好(要求每位同學只能選擇其中一種自己喜歡的球類運動),并將調查結果繪制成了如下條形統計圖和扇形統計圖(不完整).請你根據圖中提供的信息,解答下列問題: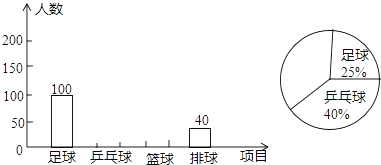
(1)本次抽樣調查,共調查了名學生;
(2)請將條形統計圖和扇形統計圖補充完整;
(3)若該學校共有學生1800人,根據以上數據分析,試估計選擇排球運動的同學約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=BC,BE⊥AC于點E,AD⊥BC于點D,∠BAD=45°,AD與BE交于點F,連接CF.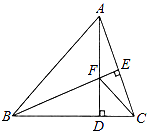
(1)求證:BF=2AE;
(2)若CD= ![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=8,BC=6,P是AC上一點,過P作PD⊥AB于點D,將△APD繞PD的中點旋轉180°得到△EPD.(設AP=x)
(1)若點E落在邊BC上,求AP的長;
(2)當AP為何值時,△EDB為等腰三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某單位準備組織員工到北京旅游,現聯系了甲、乙兩家旅行社,兩家旅行社報價均為2000元/人,同時兩家旅行社都對10人以上的團體推出了優惠舉措:甲旅行社對每位員工七五折優惠;而乙旅行社是一位員工免費,其余員工八折優惠.
(1)如果設參加旅游的員工共有a(a>10)人,則甲旅行社的費用為元,乙旅行社的費用為元;(用含a的代數式表示,并化簡)
(2)如果組織20名員工到北京旅游,該單位選擇哪一家旅行社比較優惠?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數y=﹣2x+4的圖象如圖,圖象與x軸交于點A,與y軸交于點B.
(1)求A、B兩點坐標.
(2)求圖象與坐標軸所圍成的三角形的面積是多少.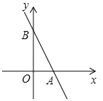
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在□ABCD中,E為BC的中點,過點E作EF⊥AB于點F,延長DC,交FE的延長線于點G,連結DF,已知∠FDG=45°
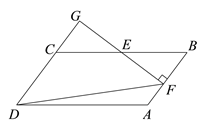
(1)求證:GD=GF.
(2)已知BC=10, ![]() .求 CD的長.
.求 CD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com