
【題目】如圖,拋物線y=ax2+bx﹣a﹣b(a<0,a、b為常數)與x軸交于A、C兩點,與y軸交于B點,直線AB的函數關系式為y= ![]() x+
x+ ![]() .
.
(1)求該拋物線的函數關系式與C點坐標;
(2)已知點M(m,0)是線段OA上的一個動點,過點M作x軸的垂線l分別與直線AB和拋物線交于D、E兩點,當m為何值時,△BDE恰好是以DE為底邊的等腰三角形?
(3)在(2)問條件下,當△BDE恰好是以DE為底邊的等腰三角形時,動點M相應位置記為點M′,將OM′繞原點O順時針旋轉得到ON(旋轉角在0°到90°之間);
i:探究:線段OB上是否存在定點P(P不與O、B重合),無論ON如何旋轉, ![]() 始終保持不變,若存在,試求出P點坐標;若不存在,請說明理由;
始終保持不變,若存在,試求出P點坐標;若不存在,請說明理由;
ii:試求出此旋轉過程中,(NA+ ![]() NB)的最小值.
NB)的最小值.
【答案】
(1)
解:在y= ![]() x+
x+ ![]() 中,令x=0,則y=
中,令x=0,則y= ![]() ,令y=0,則x=﹣6,
,令y=0,則x=﹣6,
∴B(0, ![]() ),A(﹣6,0),
),A(﹣6,0),
把B(0, ![]() ),A(﹣6,0)代入y=ax2+bx﹣a﹣b得
),A(﹣6,0)代入y=ax2+bx﹣a﹣b得  ,
,
∴  ,
,
∴拋物線的函數關系式為:y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ,
,
令y=0,則=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() =0,
=0,
∴x1=﹣6,x2=1,
∴C(1,0)
(2)
解:∵點M(m,0),過點M作x軸的垂線l分別與直線AB和拋物線交于D、E兩點,
∴D(m, ![]() m+
m+ ![]() ),當DE為底時,
),當DE為底時,
作BG⊥DE于G,則EG=GD= ![]() ED,GM=OB=
ED,GM=OB= ![]() ,
,
∴ ![]() m+
m+ ![]() (﹣
(﹣ ![]() m2﹣
m2﹣ ![]() m+
m+ ![]() +
+ ![]() m+
m+ ![]() )=
)= ![]() ,
,
解得:m1=﹣4,m2=9(不合題意,舍去),
∴當m=﹣4時,△BDE恰好是以DE為底邊的等腰三角形

(3)
解:i:存在,
∵ON=OM′=4,OB= ![]() ,
,
∵∠NOP=∠BON,
∴當△NOP∽△BON時, ![]() =
= ![]() ,
,
∴ ![]() 不變,
不變,
即OP= ![]() =3,
=3,
∴P(0,3)
ii:∵N在以O為圓心,4為半徑的半圓上,由(i)知, ![]() =
= ![]() ,
,
∴NP= ![]() NB,
NB,
∴(NA+ ![]() NB)的最小值=NA+NP,
NB)的最小值=NA+NP,
∴此時N,A,P三點共線,
∴(NA+ ![]() NB)的最小值=
NB)的最小值= ![]() =3
=3 ![]() .
.

【解析】(1)根據已知條件得到B(0, ![]() ),A(﹣6,0),解方程組得到拋物線的函數關系式為:y=﹣
),A(﹣6,0),解方程組得到拋物線的函數關系式為:y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]() ,于是得到C(1,0);(2)由點M(m,0),過點M作x軸的垂線l分別與直線AB和拋物線交于D、E兩點,得到D(m,
,于是得到C(1,0);(2)由點M(m,0),過點M作x軸的垂線l分別與直線AB和拋物線交于D、E兩點,得到D(m, ![]() m+
m+ ![]() ),當DE為底時,作BG⊥DE于G,根據等腰三角形的性質得到EG=GD=
),當DE為底時,作BG⊥DE于G,根據等腰三角形的性質得到EG=GD= ![]() ED,GM=OB=
ED,GM=OB= ![]() ,列方程即可得到結論;(3)i:根據已知條件得到ON=OM′=4,OB=
,列方程即可得到結論;(3)i:根據已知條件得到ON=OM′=4,OB= ![]() ,由∠NOP=∠BON,特殊的當△NOP∽△BON時,根據相似三角形的性質得到
,由∠NOP=∠BON,特殊的當△NOP∽△BON時,根據相似三角形的性質得到 ![]() =
= ![]() ,于是得到結論;
,于是得到結論;
ii:根據題意得到N在以O為圓心,4為半徑的半圓上,由(i)知, ![]() =
= ![]() ,得到NP=
,得到NP= ![]() NB,于是得到(NA+
NB,于是得到(NA+ ![]() NB)的最小值=NA+NP,此時N,A,P三點共線,根據勾股定理得到結論.
NB)的最小值=NA+NP,此時N,A,P三點共線,根據勾股定理得到結論.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,AD與過點C的切線互相垂直,垂足為點D,AD交⊙O于點E,連接CE,CB. 
(1)求證:CE=CB;
(2)若AC=2 ![]() ,CE=
,CE= ![]() ,求AE的長.
,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB≠AC.D、E分別為邊AB、AC上的點.AC=3AD,AB=3AE,點F為BC邊上一點,添加一個條件: , 可以使得△FDB與△ADE相似.(只需寫出一個) 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=mx2﹣16mx+48m(m>0)與x軸交于A,B兩點(點B在點A左側),與y軸交于點C,點D是拋物線上的一個動點,且位于第四象限,連接OD、BD、AC、AD,延長AD交y軸于點E.
(1)若△OAC為等腰直角三角形,求m的值;
(2)若對任意m>0,C、E兩點總關于原點對稱,求點D的坐標(用含m的式子表示);
(3)當點D運動到某一位置時,恰好使得∠ODB=∠OAD,且點D為線段AE的中點,此時對于該拋物線上任意一點P(x0 , y0)總有n+ ![]() ≥﹣4
≥﹣4 ![]() my02﹣12
my02﹣12 ![]() y0﹣50成立,求實數n的最小值.
y0﹣50成立,求實數n的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】烏江快鐵大橋是快鐵渝黔線的一項重要工程,由主橋AB和引橋BC兩部分組成(如圖所示),建造前工程師用以下方式做了測量;無人機在A處正上方97m處的P點,測得B處的俯角為30°(當時C處被小山體阻擋無法觀測),無人機飛行到B處正上方的D處時能看到C處,此時測得C處俯角為80°36′.
(長度均精確到1m,參考數據: ![]() ≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)
≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)
(1)求主橋AB的長度;
(2)若兩觀察點P、D的連線與水平方向的夾角為30°,求引橋BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“一帶一路”倡議下,我國已成為設施聯通,貿易暢通的促進者,同時也帶動了我國與沿線國家的貨物交換的增速發展,如圖是湘成物流園2016年通過“海、陸(汽車)、空、鐵”四種模式運輸貨物的統計圖. 請根據統計圖解決下面的問題:
(1)該物流園2016年貨運總量是多少萬噸?
(2)該物流園2016年空運貨物的總量是多少萬噸?并補全條形統計圖;
(3)求條形統計圖中陸運貨物量對應的扇形圓心角的度數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠AOB的一邊OA為平面鏡,∠AOB=38°,在OB上有一點E , 從E點射出一束光線經OA上一點D反射,反射光線DC恰好與OB平行,則∠DEB的度數是( )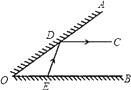
A.76°
B.52°
C.45°
D.38°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某網店嘗試用單價隨天數而變化的銷售模式銷售一種商品,利用30天的時間銷售一種成本為10元/件的商品售后,經過統計得到此商品單價在第x天(x為正整數)銷售的相關信息,如表所示:
銷售量n(件) | n=50﹣x |
銷售單價m(元/件) | 當1≤x≤20時, |
當21≤x≤30時, |
(1)請計算第15天該商品單價為多少元/件?
(2)求網店銷售該商品30天里所獲利潤y(元)關于x(天)的函數關系式;
(3)這30天中第幾天獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,AD∥BC,AD=AB=DC= ![]() BC=1,E是PC的中點,面PAC⊥面ABCD.
BC=1,E是PC的中點,面PAC⊥面ABCD. 
(Ⅰ)證明:ED∥面PAB;
(Ⅱ)若PC=2,PA= ![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com