
已知:如圖,以△ABC的一邊BC為直徑的⊙O分別交AB、AC于D、E兩點.
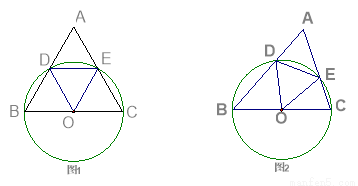
(1)當△ABC為等邊三角形時,則圖1中△ODE的形狀是 ;
(2)若?A=60°,AB≠AC(如圖2),則(1)的結論是否還成立?請說明理由.
(1)△ODE為等邊三角形(2)成立
【解析】
試題分析:(1)根據等邊三角形的性質知?B=?C=60°,再結合同圓的半徑相等,可知OB=OC=OD=OE,進而知△OBD,△OEC均為等邊三角形,所以?BOD=?COE=60°,再由平角的定義知?DOE=60°,因此得證;
(2)連接CD,由BC為⊙O直徑,可根據直徑所對的圓周角是直角,可得CD⊥AB,所以可求得∠ACD=30°,再根據同弧所對的圓周角等于其所對的圓心角的一半的性質可求得∠DOE=60°,再由半徑相等得證結論成立.
試題解析:【解析】
△ODE為等邊三角形
證明:∵△ABC為等邊三角形,
∴?B=?C=60°.
∵OB=OC=OD=OE,
∴△OBD,△OEC均為等邊三角形.
∴?BOD=?COE=60°.
∴?DOE=60°.
∵OD=OE,
∴△ODE為等邊三角形.
(2)答:成立.
證明:如圖:連接CD
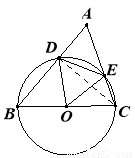
∵BC為⊙O直徑,
∴?BDC=90°,
∴?ADC=90°.
∵?A=60°,
∴?ACD=30°.
∴?DOE=60°.
∵OD=OE,
∴△DOE為等邊三角形.
考點:等邊三角形,圓周角的性質定理


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:2014-2015學年北京市東城區九年級上學期期末考試數學試卷(解析版) 題型:解答題
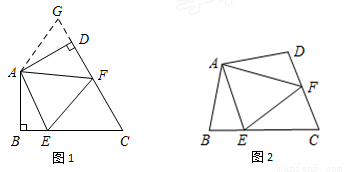
(1)如圖1,在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,EF分別是 BC,CD上的點,且∠EAF=60°,探究圖中線段BE,EF,FD之間的數量關系.
小王同學探究此問題的方法是延長FD到點G,使DG=BE,連結AG,先證明△ABE≌△ADG,再證明△AEF≌△AGF,可得出結論,他的結論應是 ;
探索延伸:
(2)如圖2,若在四邊形ABCD中,AB=AD,∠B+∠D=180°,E,F分別是BC,CD上的點,且∠EAF=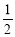 ∠BAD,上述結論是否仍然成立,并說明理由.
∠BAD,上述結論是否仍然成立,并說明理由.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年北京市東城區九年級上學期期末考試數學試卷(解析版) 題型:選擇題
如圖,線段AB是⊙O的直徑,弦CD丄AB,∠CAB=20°,則∠AOD等于( )
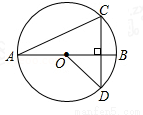
A.120° B.140° C.150° D.160°
查看答案和解析>>
科目:初中數學 來源:2014-2015學年北京市大興區九年級上學期期末考試數學試卷(解析版) 題型:解答題
已知:如圖,二次函數y=a(x﹣h)2+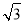 的圖象經過原點O(0,0),A(2,0).
的圖象經過原點O(0,0),A(2,0).
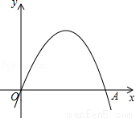
(1)寫出該函數圖象的對稱軸;
(2)若將線段OA繞點O逆時針旋轉60°到OA′,試判斷點A′是否為該函數圖象的頂點?請說明理由.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年北京市大興區九年級上學期期末考試數學試卷(解析版) 題型:選擇題
在一個口袋中有4個完全相同的小球,把它們分別標號為①,②,③,④,隨機地摸出一個小球,記錄后放回,再隨機摸出一個小球,則兩次摸出的小球的標號相同的概率是( )
A.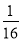 B.
B.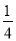 C.
C.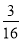 D.
D.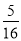
查看答案和解析>>
科目:初中數學 來源:2014-2015學年重慶市七年級上學期期末考試數學試卷(解析版) 題型:解答題
列方程解應用題 (10分)
甲、乙兩人同時從相距25千米的A地去B 地,甲騎車乙步行,甲的速度是乙的速度的3倍,甲到達B地停留40分鐘,然后從B地返回A地,在途中遇見乙,這時距他們出發的時間恰好3小時,求兩人的速度各是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com