
【題目】如圖,直線AB、CD相交于點O,OE平分∠BOD,OF平分∠COE,∠AOD:∠BOD=2:1 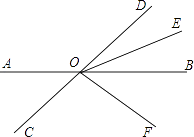
(1)求∠DOE的度數;
(2)求∠AOF的度數.
【答案】
(1)解:∵∠AOD:∠BOD=2:1,∠AOD+∠BOD=180°,
∴∠BOD= ![]() ×180°=60°,
×180°=60°,
∵OE平分∠BOD,
∴∠DOE= ![]() ∠BOD=
∠BOD= ![]() ×60°=30°
×60°=30°
(2)解:∠COE=∠COD﹣∠DOE=180°﹣30°=150°,
∵OF平分∠COE,
∴∠COF= ![]() ∠COE=
∠COE= ![]() ×150°=75°,
×150°=75°,
∵∠AOC=∠BOD=60°(對頂角相等),
∴∠AOF=∠AOC+∠COF=60°+75°=135°
【解析】(1)根據鄰補角的和等于180°求出∠BOD的度數,然后根據角平分線的定義解答;(2)先求出∠COE的度數,再根據角平分線的定義求出∠COF,然后根據對頂角相等求出∠AOC,再根據∠AOF=∠AOC+∠COF,代入數據進行計算即可得解.
【考點精析】關于本題考查的角的平分線和對頂角和鄰補角,需要了解從一個角的頂點引出的一條射線,把這個角分成兩個相等的角,這條射線叫做這個角的平分線;兩直線相交形成的四個角中,每一個角的鄰補角有兩個,而對頂角只有一個才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】有理數a,b,c在數軸上對應的點如圖所示,則下列式子中正確的是( ) ![]()
A.a>b
B.|a﹣c|=a﹣c
C.﹣a<﹣b<c
D.|b+c|=b+c
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】體育老師對甲、乙兩名同學分別進行了8次跳高測試,經計算這兩名同學成績的平均數相同,甲同學的方差是S甲2=6.4,乙同學的方差是S乙2=8.2,那么這兩名同學跳高成績比較穩定的是同學.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】以下四個命題:
①若一個角的兩邊和另一個角的兩邊分別互相垂直,則這兩個角互補;
②邊數相等的兩個正多邊形一定相似;
③等腰三角形ABC中,D是底邊BC上一點,E是一腰AC上的一點,若∠BAD=60°且AD=AE,則∠EDC=30°;
④任意三角形的外接圓的圓心一定是三角形三條邊的垂直平分線的交點.
其中正確命題的序號為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有多個全等直角三角形,先取三個拼成如圖1所示的形狀,R為DE的中點,BR分別交AC,CD于P,Q,易得BP:QP:QR=3:1:2.
(1)若取四個直角三角形拼成如圖2所示的形狀,S為EF的中點,BS分別交AC,CD,DE于P,Q,R,則BP:PQ:QR:RS=
(2)若取五個直角三角形拼成如圖3所示的形狀,T為FG的中點,BT分別交AC,CD,DE,EF于P,Q,R,S,則BP:PQ:QR:RS:ST= .
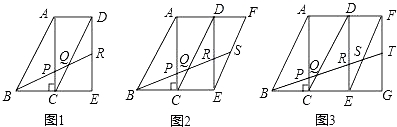
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把△ABC紙片沿DE折疊,當點A在四邊形BCDE的外部時,記∠AEB為∠1,∠ADC為∠2,則∠A、∠1與∠2的數量關系,結論正確的是( )

A. ∠1=∠2+∠A B. ∠1=2∠A+∠2
C. ∠1=2∠2+2∠A D. 2∠1=∠2+∠A
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:
小明在學習二次根式后,發現一些含根號的式子可以寫成另一個式子的平方,如3+2![]() =(1+
=(1+![]() )2.善于思考的小明進行了以下探索:
)2.善于思考的小明進行了以下探索:
設a+b![]() =(m+n
=(m+n![]() )2(其中a、b、m、n均為整數),則有a+b
)2(其中a、b、m、n均為整數),則有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.這樣小明就找到了一種把類似a+b![]() 的式子化為平方式的方法.
的式子化為平方式的方法.
請你仿照小明的方法探索并解決下列問題:
(1)當a、b、m、n均為正整數時,若a+b![]() =
=![]() ,用含m、n的式子分別表示a、b,得:a=__,b=__;
,用含m、n的式子分別表示a、b,得:a=__,b=__;
(2)利用所探索的結論,找一組正整數a、b、m、n填空:__+__![]() =(___)+__
=(___)+__![]() )2;
)2;
(3)若a+4![]() =
=![]() ,且a、m、n均為正整數,求a的值?
,且a、m、n均為正整數,求a的值?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com