
【題目】二次函數![]() (
(![]() )的圖象如圖所示,對稱軸為直線
)的圖象如圖所示,對稱軸為直線![]() ,有下列結論:①
,有下列結論:①![]() ;②
;②![]() ;③
;③![]() .其中,正確結論的個數是( )
.其中,正確結論的個數是( )
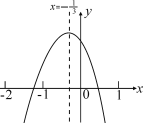
A.3個B.2個C.1個D.0個
【答案】A
【解析】
根據二次函數的圖象的位置,確定a、b、c的符號,通過對稱軸,與x軸交點的位置確定各個選項的正確與錯誤即可.
解:拋物線開口向下,因此a<0,對稱軸在y軸的左側,a、b同號,故b<0,與y軸的交點在y軸的正半軸,因此c>0,
故abc>0,因此①正確,
對稱軸為x=![]() -
-![]() ,即2a=3b,也就是
,即2a=3b,也就是![]() ,
,
由圖象可知,當x=-1時,y=a-b+c>0,即![]() >0,
>0,
則有b+2c>0,所以②正確,
當x=-2時,y=4a-2b+c<0,①
當x=1時,y=a+b+c<0,②
①+②得,5a-b+2c<0,
又2a=3b,則4a=6b,
∴5a-b+2c=a+4a-b+2c=a+5b+2c<0,
因此③正確,
故選:A.


 學業測評一課一測系列答案
學業測評一課一測系列答案 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案科目:初中數學 來源: 題型:
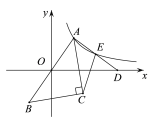
【題目】如圖,點A與點B關于原點對稱,點C在第四象限,∠ACB=90°.點D是![]() 軸正半軸上一點,AC平分∠BAD,E是AD的中點,反比例函數
軸正半軸上一點,AC平分∠BAD,E是AD的中點,反比例函數![]() (
(![]() )的圖象經過點A,E.若△ACE的面積為6,則
)的圖象經過點A,E.若△ACE的面積為6,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在銳角△ABC中,AB=4,BC=5,∠ACB=45°,將△ABC繞點B按逆時針方向旋轉,得到△A1BC1.
(1)如圖1,當點C1在線段CA的延長線上時,求∠CC1A1的度數;
(2)如圖2,連接AA1,CC1.若△ABA1的面積為4,求△CBC1的面積;
(3)如圖3,點E為線段AB中點,點P是線段AC上的動點,在△ABC繞點B按逆時針方向旋轉過程中,點P的對應點是點P1,求線段EP1長度的最大值與最小值.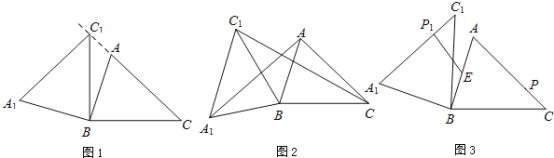
查看答案和解析>>
科目:初中數學 來源: 題型:
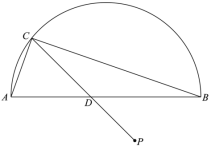
【題目】如圖,![]() 是半圓的直徑,P是半圓與直徑
是半圓的直徑,P是半圓與直徑![]() 所圍成的圖形的外部的一定點,D是直徑
所圍成的圖形的外部的一定點,D是直徑![]() 上一動點,連接
上一動點,連接![]() 并延長,交半圓于點C,連接
并延長,交半圓于點C,連接![]() .已知
.已知![]() ,設
,設![]() 兩點間的距離為
兩點間的距離為![]() ,
,![]() 兩點之間的距離為
兩點之間的距離為![]() 兩點之間的距離為
兩點之間的距離為![]() .
.
小明根據學習函數的經驗,分別對函數![]() 隨自變量x的變化而變化的規律進行了探究.
隨自變量x的變化而變化的規律進行了探究.
下面是小明的探究過程,請補充完整:
(1)按照下表自變量x的值進行取點、畫圖、測量,分別得到![]() 與x的幾組對應值;
與x的幾組對應值;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 0.47 | 1.31 | 5.02 | 5.91 | 6 | |
| 6 | 5.98 | 5.86 | 5.26 | 3.29 | 1.06 | 0 |
(2)在同一平面直角坐標系![]() 中,描出補全后的表中各組數值所對應的點
中,描出補全后的表中各組數值所對應的點![]() ,
,![]() ,并畫出函數
,并畫出函數![]() 的圖象;
的圖象;
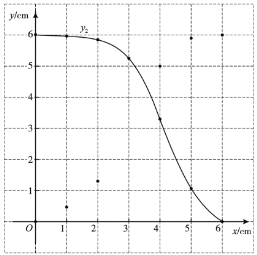
(3)結合函數圖象,解決問題:當![]() 有一個角的正弦值為
有一個角的正弦值為![]() 時,
時,![]() 的長約為_____cm.
的長約為_____cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有兩個旅游公司經營某景點的門票銷售.甲公司只經營散客門票,票價為40元∕張;乙公司只經營團體票,一次購買門票不超過10張,票價為50元∕張,一次性購買門票超過10張時,其中有10張門票的票價仍為50元∕張,超出10張部分的票價為30元∕張.某班部分同學要去該景點旅游,設參加旅游的學生有![]() 人(
人(![]() 為非負整數).
為非負整數).
(1)根據題意填表:
一次購買門票數量∕張 |
|
|
| … |
甲旅游公司費用∕元 |
| … | ||
乙旅游公司費用∕元 |
| … |
(2)設去甲旅游公司購買門票費用為![]() 元,去乙旅游公司購買門票費用為
元,去乙旅游公司購買門票費用為![]() 元,分別求
元,分別求![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(3)根據題意填空:
①若在甲公司和在乙公司購買門票的數量相同,且費用相同,則在同一個旅游公司一次購買門票的數量為 張;
②若在同一個旅游公司一次購買門票![]() 張,則在甲、乙兩個旅游公司中的 公司購買花費少;
張,則在甲、乙兩個旅游公司中的 公司購買花費少;
③若在同一個旅游公司一次購買門票花費了![]() 元,則在甲、乙兩個旅游公司中 公司購買門票數量多.
元,則在甲、乙兩個旅游公司中 公司購買門票數量多.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解學生參加體育活動的情況,學校對學生進行隨機抽樣調查,其中一個問題是“你平均每天參加體育活動的時間是多少”,共有4個選項:A 1.5小時以上;B 1~1.5小時;C 0.5~1小時;D 0.5小時以下.圖1、2是根據調查結果繪制的兩幅不完整的統計圖,請你根據統計圖提供的信息,解答以下問題:

(1)本次一共調查了多少名學生?
(2)在圖1中將選項B的部分補充完整;
(3)若該校有3000名學生,你估計全校可能有多少名學生平均每天參加體育活動的時間在0.5小時以下.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,樓頂有一根天線,為了測量樓的高度,在地面上取成一條直線的三點E、D、C,在點C處測得天線頂端A的仰角為60°,從點C走到點D,CD=6米,從點D處測得天線下端B的仰角為45°.又知A、B、E在一條線上,AB=25米,求樓高BE.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB = 90,D為AB的中點,AE∥DC,CE∥DA.
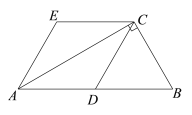
(1)求證:四邊形ADCE是菱形;
(2)連接DE,若AC =![]() ,BC =2,求證:△ADE是等邊三角形.
,BC =2,求證:△ADE是等邊三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com