
如圖,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果點P由B出發沿BA向點A勻速運動,同時點Q由A出發沿AC向點C勻速運動,它們的速度均為2cm/s.連接PQ,設運動的時間為t(單位:s)(0≤t≤4).
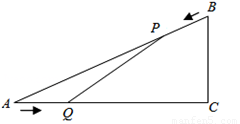
(1)當t為何值時,PQ∥BC.
(2)設△AQP的面積為S(單位:cm2),當t為何值時,S取得最大值,并求出最大值.
(3)是否存在某時刻t,使線段PQ恰好把△ABC的面積平分?若存在,求出此時t的值;若不存在,請說明理由.
(1) s;(2)t=
s;(2)t= s時,S取得最大值為
s時,S取得最大值為 cm2;(3)不存在
cm2;(3)不存在
【解析】
試題分析:(1)由PQ∥BC可得 ,即
,即 ,解出即可;
,解出即可;
(2)先根據勾股定理的逆定理證得∠C=90°,過P點作PD⊥AC于點D,則PD∥BC, ,即
,即 ,解得PD=6﹣
,解得PD=6﹣ t,即可得到S關于t的二次函數,根據二次函數的性質即可求得結果;
t,即可得到S關于t的二次函數,根據二次函數的性質即可求得結果;
(3)假設存在某時刻t,使線段PQ恰好把△ABC的面積平分,則有S△AQP= S△ABC=12.由(2)可知,S△AQP=﹣
S△ABC=12.由(2)可知,S△AQP=﹣ t2+6t,則有﹣
t2+6t,則有﹣ t2+6t=12,根據此方程無解,即可作出判斷.
t2+6t=12,根據此方程無解,即可作出判斷.
(1)∵PQ∥BC
∴
即
解得t=
∴當t= s時,PQ∥BC
s時,PQ∥BC
(2)∵AB=10cm,AC=8cm,BC=6cm,
∴∠C=90°
過P點作PD⊥AC于點D.

∴PD∥BC,
∴ ,
,
即 ,
,
解得PD=6﹣ t
t
∴S= ×AQ×PD=
×AQ×PD= ×2t×(6﹣
×2t×(6﹣ t)
t)
=﹣ t2+6t=﹣
t2+6t=﹣ (t﹣
(t﹣ )2+
)2+ ,
,
∴當t= s時,S取得最大值,最大值為
s時,S取得最大值,最大值為 cm2
cm2
(3)假設存在某時刻t,使線段PQ恰好把△ABC的面積平分,
則有S△AQP= S△ABC=12.
S△ABC=12.
由(2)可知,S△AQP=﹣ t2+6t,
t2+6t,
∴﹣ t2+6t=12,
t2+6t=12,
化簡得:t2﹣5t+10=0,
∵△=(﹣5)2﹣4×1×10=﹣15<0,此方程無解,
∴不存在某時刻t,使線段PQ恰好把△ABC的面積平分.
考點:動點的綜合題
點評:此類問題綜合性強,難度較大,在中考中比較常見,一般作為壓軸題,題目比較典型.


科目:初中數學 來源: 題型:
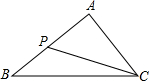 如圖,已知△ABC中,P是AB上一點,連接CP,以下條件不能判定△ACP∽△ABC的是( )
如圖,已知△ABC中,P是AB上一點,連接CP,以下條件不能判定△ACP∽△ABC的是( )
|
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知△ABC中,BC=8,BC邊上的高h=4,D為BC上一點,EF∥BC交AB于E,交AC于F(EF不過A、B),設E到BC的距離為x,△DEF的面積為y,那么y關于x的函數圖象大致是( )
如圖,已知△ABC中,BC=8,BC邊上的高h=4,D為BC上一點,EF∥BC交AB于E,交AC于F(EF不過A、B),設E到BC的距離為x,△DEF的面積為y,那么y關于x的函數圖象大致是( )



查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知△ABC中,AB=AC,D是BC中點,則下列結論不正確的是( )
如圖,已知△ABC中,AB=AC,D是BC中點,則下列結論不正確的是( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com