
【題目】如圖,O為直線AB上一點,OD平分∠AOC,∠DOE=90°.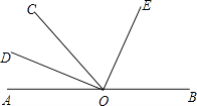
(1)請你數一數,圖中有個小于平角的角;
(2)若∠AOC=50°,則∠COE的度數= , ∠BOE的度數=;
(3)猜想:OE是否平分∠BOC?請通過計算說明你猜想的結論.
【答案】
(1)9
(2)65°,65°
(3)解:結論:OE平分∠BOC.
理由:設∠AOC=2α,
∵OD平分∠AOC,∠AOC=2α,
∴∠AOD=∠COD= ![]() ∠AOC=α,
∠AOC=α,
又∵∠DOE=90°
∴∠COE=∠DOE﹣∠COD=90°﹣α.
又∵∠BOE=180°﹣∠DOE﹣∠AOD=180°﹣90°﹣α=90°﹣α,
∴∠COE=∠BOE,即OE平分∠BOC.
【解析】解:(1)∠AOD、∠COA、∠AOE、∠DOC、∠DOE、∠DOB、∠COE、∠COB、∠EOB共9個;
(2)∵OD平分∠AOC,
∴∠COD=∠AOD=![]() ∠AOC=50°,
∠AOC=50°,
∴∠COE=∠DOE-∠COD=90°-25°=65°,
∴∠BOE=180°-∠AOD-∠DOE=180°-25°-90°=65°.
(1)直接結合圖形可寫出所有的角;
(2)先角平分線的定義可求出∠COD、∠AOD的度數,再由∠COE=∠DOE-∠COD、∠BOE=180°-∠AOD-∠DOE可分別求出答案;
(3)設∠AOC=2α,利用平分線的定義可表示出∠AOD、∠COD,同(2)可表示出∠COE、∠BOE,進而可得答案.


科目:初中數學 來源: 題型:
【題目】如圖,已知∠ABC=∠BAD,添加下列條件還不能判定△ABC≌△BAD的是( )
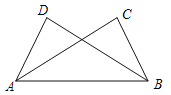
A.AC=BD B.∠CAB=∠DBA C.∠C=∠D D.BC=AD
查看答案和解析>>
科目:初中數學 來源: 題型:
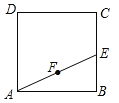
【題目】如圖,正方形ABCD的面積為3cm2,E為BC邊上一點,∠BAE=30°,F為AE的中點,過點F作直線分別與AB,DC相交于點M,N.若MN=AE,則AM的長等于 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
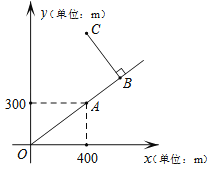
【題目】如圖是根據某公園的平面示意圖建立的平面直角坐標系,公園的入口位于坐標原點O,古塔位于點A(400,300),從古塔出發沿射線OA方向前行300m是盆景園B,從盆景園B向左轉90°后直行400m到達梅花閣C,則點C的坐標是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD的四邊相等,且面積為120cm2 , 對角線AC=24cm,則四邊形ABCD的周長為( ) 
A.52cm
B.40cm
C.39cm
D.26cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCD沿BD對折,點A落在E處,BE與CD相交于F,若AD=3,BD=6. 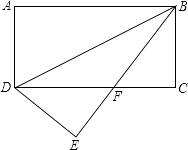
(1)求證:△EDF≌△CBF;
(2)求∠EBC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com