
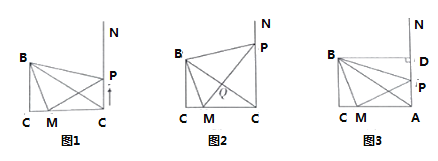
【題目】如圖,D是△ABC外接圓上的動點,且B,D位于AC的兩側,DE⊥AB,垂足為E,DE的延長線交此圓于點F.BG⊥AD,垂足為G,BG交DE于點H,DC,FB的延長線交于點P,且PC=PB.
(1)求證:BG∥CD;
(2)設△ABC外接圓的圓心為O,若AB=![]() DH,∠OHD=80°,求∠BDE的大小.
DH,∠OHD=80°,求∠BDE的大小.
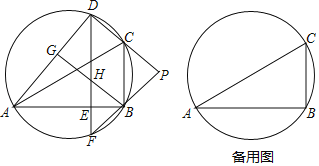
【答案】(1)證明見解析;(2)20°或40°.
【解析】
(1)根據等邊對等角得:∠PCB=∠PBC,由四點共圓的性質得:∠BAD+∠BCD=180°,從而得:∠BFD=∠PCB=∠PBC,根據平行線的判定得:BC∥DF,可得∠ABC=90°,AC是⊙O的直徑,從而得:∠ADC=∠AGB=90°,根據同位角相等可得結論;
(2)先證明四邊形BCDH是平行四邊形,得BC=DH,根據特殊的三角函數值得:∠ACB=60°,∠BAC=30°,所以DH=![]() AC,分兩種情況:
AC,分兩種情況:
①當點O在DE的左側時,如圖2,作輔助線,構建直角三角形,由同弧所對的圓周角相等和互余的性質得:∠AMD=∠ABD,則∠ADM=∠BDE,并由DH=OD,可得結論;
②當點O在DE的右側時,如圖3,同理作輔助線,同理有∠ADE=∠BDN=20°,∠ODH=20°,得結論.
(1)證明:如圖1,
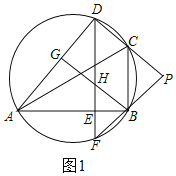
∵PC=PB,
∴∠PCB=∠PBC,
∵四邊形ABCD內接于圓,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直徑,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(2)由(1)得:BC∥DF,BG∥CD,
∴四邊形BCDH是平行四邊形,
∴BC=DH,
在Rt△ABC中,∵AB=![]() DH,
DH,
∴tan∠ACB=![]() ,
,
∴∠ACB=60°,∠BAC=30°,
∴∠ADB=60°,BC=![]() AC,
AC,
∴DH=![]() AC,
AC,
①當點O在DE的左側時,如圖2,作直徑DM,連接AM、OH,則∠DAM=90°,
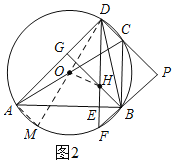
∴∠AMD+∠ADM=90°
∵DE⊥AB,
∴∠BED=90°,
∴∠BDE+∠ABD=90°,
∵∠AMD=∠ABD,
∴∠ADM=∠BDE,
∵DH=![]() AC,
AC,
∴DH=OD,
∴∠DOH=∠OHD=80°,
∴∠ODH=20°
∵∠AOB=60°,
∴∠ADM+∠BDE=40°,
∴∠BDE=∠ADM=20°,
②當點O在DE的右側時,如圖3,作直徑DN,連接BN,
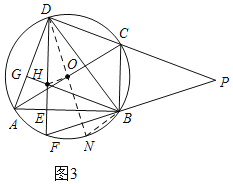
由①得:∠ADE=∠BDN=20°,∠ODH=20°,
∴∠BDE=∠BDN+∠ODH=40°,
綜上所述,∠BDE的度數為20°或40°.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數學 來源: 題型:
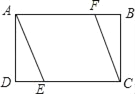
【題目】如圖,矩形ABCD中,AD=2,AB=3,過點A,C作相距為2的平行線段AE,CF,分別交CD,AB于點E,F,則DE的長是( )
A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
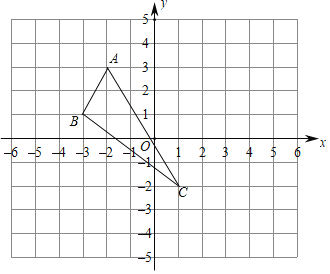
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點的位置如圖所示.
(1)若△ABC內有一點P(a,b)隨著△ABC平移后到了點P′(a+4,b﹣1),直接寫出A點平移后對應點A′的坐標.
(2)直接作出△ABC關于y軸對稱的△A′B′C′(其中A′、B′、C′分別是A、B、C的對應點)
(3)求四邊形ABC′C的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() .動點
.動點![]() 從
從![]() 的頂點
的頂點![]() 出發,以
出發,以![]() 的速度沿
的速度沿![]() 勻速運動回到點
勻速運動回到點![]() .圖2是點
.圖2是點![]() 運動過程中,線段
運動過程中,線段![]() 的長度
的長度![]() 隨時間
隨時間![]() 變化的圖象.其中點
變化的圖象.其中點![]() 為曲線部分的最低點.
為曲線部分的最低點.
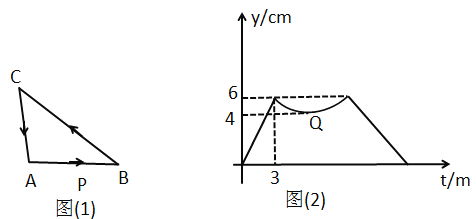
請從下面A、B兩題中任選一作答,我選擇________題.
A.![]() 的面積是______,B.圖2中
的面積是______,B.圖2中![]() 的值是______.
的值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,平面直角坐標系中,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于點
軸分別交于點![]() ,
,![]() ,直線
,直線![]() 經過點
經過點![]() ,并與
,并與![]() 軸交于點
軸交于點![]() .
.
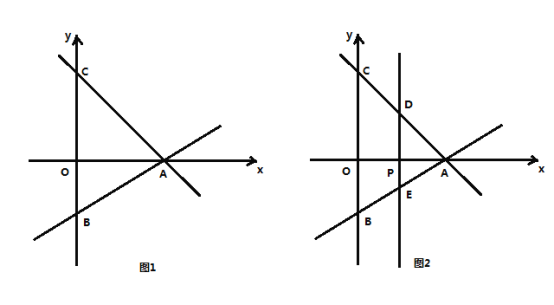
(1)求![]() ,
,![]() 兩點的坐標及
兩點的坐標及![]() 的值;
的值;
(2)如圖2,動點![]() 從原點
從原點![]() 出發,以每秒
出發,以每秒![]() 個單位長度的速度沿
個單位長度的速度沿![]() 軸正方向運動.過點
軸正方向運動.過點![]() 作
作![]() 軸的垂線,分別交直線
軸的垂線,分別交直線![]() ,
,![]() 于點
于點![]() ,
,![]() .設點
.設點![]() 運動的時間為
運動的時間為![]() .
.
①點![]() 的坐標為______.點
的坐標為______.點![]() 的坐標為_______;(均用含
的坐標為_______;(均用含![]() 的式子表示)
的式子表示)
②請從下面A、B兩題中任選一題作答我選擇________題.
A.當點![]() 在線段
在線段![]() 上時,探究是否存在某一時刻,使
上時,探究是否存在某一時刻,使![]() ?若存在,求出此時
?若存在,求出此時![]() 的面積;若不存在說明理由.
的面積;若不存在說明理由.
B.點![]() 是線段
是線段![]() 上一點.當點
上一點.當點![]() 在射線
在射線![]() 上時,探究是否存在某一時刻使
上時,探究是否存在某一時刻使![]() ?若存在、求出此時
?若存在、求出此時![]() 的值,并直接寫出此時
的值,并直接寫出此時![]() 為等腰三角形時點
為等腰三角形時點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把正方形鐵片OABC置于平面直角坐標系中,頂點A的坐標為(3,0),點P(1,2)在正方形鐵片上,將正方形鐵片繞其右下角的頂點按順時針方向依次旋轉90°,第一次旋轉至圖①位置,第二次旋轉至圖②位置…,則正方形鐵片連續旋轉2017次后,點P的坐標為____________________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 在
在![]() 上,且
上,且![]() ,過點
,過點![]() 作射線
作射線![]() (AN與BC在AC同側),若動點
(AN與BC在AC同側),若動點![]() 從點
從點![]() 出發,沿射線
出發,沿射線![]() 勻速運動,運動速度為
勻速運動,運動速度為![]() /
/![]() ,設點
,設點![]() 運動時間為
運動時間為![]() 秒.
秒.
(1)經過_______秒時,![]() 是等腰直角三角形?
是等腰直角三角形?
(2)當![]() 于點
于點![]() 時,求此時
時,求此時![]() 的值;
的值;
(3)過點![]() 作
作![]() 于點
于點![]() ,已知
,已知![]() ,請問是否存在點
,請問是否存在點![]() ,使
,使![]() 是以
是以![]() 為腰的等腰三角形?對存在的情況,請求出t的值,對不存在的情況,請說明理由.
為腰的等腰三角形?對存在的情況,請求出t的值,對不存在的情況,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
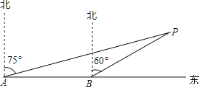
【題目】已知:如圖,為了躲避臺風,一輪船一直由西向東航行,上午![]() 點,在
點,在![]() 處測得小島
處測得小島![]() 的方向是北偏東
的方向是北偏東![]() ,以每小時
,以每小時![]() 海里的速度繼續向東航行,中午
海里的速度繼續向東航行,中午![]() 點到達
點到達![]() 處,并測得小島
處,并測得小島![]() 的方向是北偏東
的方向是北偏東![]() ,若小島周圍
,若小島周圍![]() 海里內有暗礁,問該輪船是否能一直向東航行?
海里內有暗礁,問該輪船是否能一直向東航行?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a、b、c都是常數,且a≠0)的圖象與x軸交于點(﹣2,0)、(x1,0),且1<x1<2,與y軸的正半軸的交點在(0,2)的下方,下列結論:①4a﹣2b+c=0;②a<b<0;③2a+c>0;④2a﹣b+1>0.其中正確結論的個數是( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com