
 ,
, 是拋物線
是拋物線 (a ≠ 0)上不同的兩點,證明直線
(a ≠ 0)上不同的兩點,證明直線 為此拋物線的對稱軸.
為此拋物線的對稱軸.
|
 ,
, 是拋物線
是拋物線 (a ≠ 0)上不同的兩點, ∴
(a ≠ 0)上不同的兩點, ∴ 且
且  ≠
≠ .
.  .
. .
. .
. (a ≠ 0)的對稱軸為
(a ≠ 0)的對稱軸為 ,
, 為此拋物線的對稱軸.
為此拋物線的對稱軸.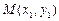 ,
,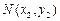 是拋物線
是拋物線 (a ≠ 0)上不同的兩點,直線
(a ≠ 0)上不同的兩點,直線 為該拋物線的對稱軸,那么自變量取
為該拋物線的對稱軸,那么自變量取 ,
, 時函數值相等嗎?寫出你的猜想,并參考上述方法寫出證明過程;
時函數值相等嗎?寫出你的猜想,并參考上述方法寫出證明過程; 當x = 4 時的函數值與x = 2007 時的函數值相等,求x = 2012時的函數值.
當x = 4 時的函數值與x = 2007 時的函數值相等,求x = 2012時的函數值.  ,
, 時函數值相等. …………………1分
時函數值相等. …………………1分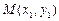 ,
,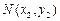 為拋物線
為拋物線 上不同的兩點,
上不同的兩點,
|
 且
且 ≠
≠ . ①-②,得
. ①-②,得  .
.  是拋物線
是拋物線 (a ≠ 0)的對稱軸,
(a ≠ 0)的對稱軸, .
. .
. ,即
,即 .………………3分
.………………3分 當x = 4 時的函數值與x = 2007 時的函數值相等,
當x = 4 時的函數值與x = 2007 時的函數值相等, 的對稱軸為直線
的對稱軸為直線 .
. ,
, .
. . …………………………………4分
. …………………………………4分 ,
,  時的函數值相等.
時的函數值相等. 時的函數值為
時的函數值為 ,
,

 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:初中數學 來源: 題型:閱讀理解
| x1+x2 |
| 2 |
|
| b |
| a |
| b |
| 2a |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
| x1+x2 |
| 2 |
|
| b |
| a |
| b |
| 2a |
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:初中數學 來源:2011屆北京市門頭溝區初三第一學期期末數學卷 題型:解答題
請閱讀下面材料:
若 ,
, 是拋物線
是拋物線 (a ≠ 0)上不同的兩點,證明直線
(a ≠ 0)上不同的兩點,證明直線 為此拋物線的對稱軸.
為此拋物線的對稱軸.
有一種方法證明如下:
|
 ,
, 是拋物線
是拋物線 (a ≠ 0)上不同的兩點, ∴
(a ≠ 0)上不同的兩點, ∴ 且
且  ≠
≠ .
.  .
. .
. .
. (a ≠ 0)的對稱軸為
(a ≠ 0)的對稱軸為 ,
, 為此拋物線的對稱軸.
為此拋物線的對稱軸.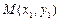 ,
, 是拋物線
是拋物線 (a ≠ 0)上不同的兩點,直線
(a ≠ 0)上不同的兩點,直線 為該拋物線的對稱軸,那么自變量取
為該拋物線的對稱軸,那么自變量取 ,
, 時函數值相等嗎?寫出你的猜想,并參考上述方法寫出證明過程;
時函數值相等嗎?寫出你的猜想,并參考上述方法寫出證明過程; 當x = 4 時的函數值與x = 2007 時的函數值相等,求x = 2012時的函數值.
當x = 4 時的函數值與x = 2007 時的函數值相等,求x = 2012時的函數值.查看答案和解析>>
科目:初中數學 來源:2010-2011學年江蘇省南通市如東縣九年級(上)期末數學試卷(解析版) 題型:解答題
 為此拋物線的對稱軸.
為此拋物線的對稱軸. 且 x1≠x2.
且 x1≠x2.
 ,
, 為此拋物線的對稱軸.
為此拋物線的對稱軸. 為該拋物線的對稱軸,那么自變量取x1,x2時函數值相等嗎?寫出你的猜想,并參考上述方法寫出證明過程;
為該拋物線的對稱軸,那么自變量取x1,x2時函數值相等嗎?寫出你的猜想,并參考上述方法寫出證明過程;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com