
閱讀下列材料:
我們知道,一次函數y=kx+b的圖象是一條直線,而y=kx+b經過恒等變形可化為直線的另一種表達形式:Ax+Bx+C=0(A、B、C是常數,且A、B不同時為0).如圖1,點P(m,n)到直線l:Ax+Bx+C=0的距離(d)計算公式是:d= .
.
例:求點P(1,2)到直線y= x-
x- 的距離d時,先將y=
的距離d時,先將y= x-
x- 化為5x-12y-2=0,再由上述距離公式求得d=
化為5x-12y-2=0,再由上述距離公式求得d= =
= .
.
解答下列問題:
如圖2,已知直線y=- x-4與x軸交于點A,與y軸交于點B,拋物線y=x2-4x+5上的一點M(3,2).
x-4與x軸交于點A,與y軸交于點B,拋物線y=x2-4x+5上的一點M(3,2).
(1)求點M到直線AB的距離.
(2)拋物線上是否存在點P,使得△PAB的面積最小?若存在,求出點P的坐標及△PAB面積的最小值;若不存在,請說明理由.
(1) 6 (2)存在,P( ,
,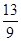 ),△PAB面積的最小值為
),△PAB面積的最小值為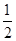 ×5×
×5×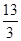 =
=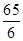
解析試題分析:(1)將y=- x-4化為4x+3y+12=0,由上述距離公式得:
x-4化為4x+3y+12=0,由上述距離公式得:
d=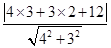 =6
=6
∴點M到直線AB的距離為6
(2)存在
設P(x,x2-4x+5),則點P到直線AB的距離為:
d=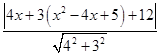
由圖象知,點P到直線AB的距離最小時x>0,x2-4x+5>0
∴d=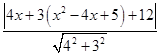 =
=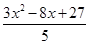 =
=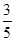 (x-
(x- )2+
)2+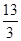
∴當x= 時,d最小,為
時,d最小,為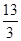
當x= 時,x2-4x+5=(
時,x2-4x+5=( )2-4×
)2-4× +5=
+5=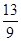 ,∴P(
,∴P( ,
,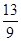 )
)
在y=- x-4中,令x=0,則y=-4,∴B(0,-4)
x-4中,令x=0,則y=-4,∴B(0,-4)
令y=0,則xy=-3。∴A(-3,0)
∴AB=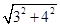 =5
=5
∴△PAB面積的最小值為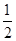 ×5×
×5×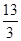 =
=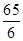
考點:直線與拋物線
點評:本題考查直線與拋物線,掌握直線與拋物線的性質,會求點到直線的距離


科目:初中數學 來源: 題型:閱讀理解
 28、
28、 閱讀下列材料:
閱讀下列材料:查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| -2+1+5 |
| 3 |
| 4 |
| 3 |
|
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| |A×m+B×n+C| | ||
|

| 5 |
| 12 |
| 1 |
| 6 |
| 5 |
| 12 |
| 1 |
| 6 |
| |5×1+(-12)×2+(-2)| | ||
|
| 21 |
| 13 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
| y |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| x |
| -x |
| x |
| -x |
|
| x2-1 |
| 1-x2 |
| x-2 |
| 2-x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com