
【題目】 若一個四邊形的兩條對角線互相垂直且相等,則稱這個四邊形為奇妙四邊形.如圖1,四邊形ABCD中,若AC=BD,AC⊥BD,則稱四邊形ABCD為奇妙四邊形.根據(jù)奇妙四邊形對角線互相垂直的特征可得奇妙四邊形的一個重要性質:奇妙四邊形的面積等于兩條對角線乘積的一半.根據(jù)以上信息回答:

(1)矩形 奇妙四邊形(填“是”或“不是”);
(2)如圖2,已知⊙O的內接四邊形ABCD是奇妙四邊形,若⊙O的半徑為6,∠ BCD=60°.求奇妙四邊形ABCD的面積;
(3)如圖3,已知⊙O的內接四邊形ABCD是奇妙四邊形作OM⊥BC于M.請猜測OM與AD的數(shù)量關系,并證明你的結論.
【答案】(1)不是;
(2)54;
(3)![]() .
.
【解析】
(1)根據(jù)矩形的性質和“奇妙四邊形”的定義進行判斷;
(2)連結OB、OD,作OH⊥BD于H,如圖2,根據(jù)垂徑定理,得到BH=DH,根據(jù)圓周角定理得到∠BOD=2∠BCD=120°,則利用等腰三角形的性質得∠OBD=30°,在Rt△OBH中可計算出![]() ,
,![]() ,則
,則![]() ,然后根據(jù)奇妙四邊形”的面積等于兩條對角線乘積的一半求解;
,然后根據(jù)奇妙四邊形”的面積等于兩條對角線乘積的一半求解;
(3)連結OB、OC、OA、OD,作OE⊥AD于E,如圖3,根據(jù)垂徑定理得到AE=DE,再利用圓周角定理得到∠BOM=∠BAC,∠AOE=∠ABD,再利用等角的余角相等得到∠OBM=∠AOE,則可證明△BOM≌△OAE得到OM=AE,于是有![]() .
.
解:(1)矩形的對角線相等但不垂直,
所以矩形不是奇妙四邊形;
故答案為:不是;
(2)

連結OB、OD,作OH⊥BD于H,如圖2,則BH=DH,
∵∠BOD=2∠BCD=2×60°=120°,
∴在等腰△OBD中,∠OBD=30°,
在Rt△OBH中,∵∠OBH=30°,
∴![]() ,
,
∴![]()
∴![]()
∵四邊形ABCD是奇妙四邊形,
∴![]() ,
,![]()
∴![]() ;
;
(3)![]() .
.
理由如下: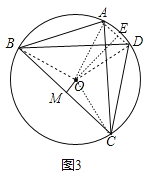
連結OB、OC、OA、OD,作OE⊥AD于E,如圖3,
∵OE⊥AD,
∴在等腰△AOD中,![]() ,
,
又∵![]() ,
,
∴∠BOM=∠BAC,
同理可得∠AOE=∠ABD,
∵BD⊥AC,
∴∠BAC+∠ABD=90°,
∴∠BOM+∠AOE=90°,
∵∠BOM+∠OBM=90°,
∴∠OBM=∠/span>AOE,
在△BOM和△OAE中

∴![]() ,
,
∴OM=AE,
∴![]() .
.


科目:初中數(shù)學 來源: 題型:
【題目】二次函數(shù)![]() 與一次函數(shù)
與一次函數(shù)![]() 在一個平面直角坐標系中.
在一個平面直角坐標系中.
(1)若二次函數(shù)![]() 的圖象頂點在一次函數(shù)
的圖象頂點在一次函數(shù)![]() 上,求
上,求![]() 的值;
的值;
(2)若當![]() 時,二次函數(shù)
時,二次函數(shù)![]() 的最小值為
的最小值為![]() ,求
,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,⊙C的半徑為r,P是與圓心C不重合的點,點P關于⊙C的發(fā)散點的定義如下:若在射線CP上存在一點P′,滿足CP+CP′=3r,則稱P′為點P關于⊙C的發(fā)散點.下圖為點P及其關于⊙C的發(fā)散點P′的示意圖.特別地,當點P′與圓心C重合時,規(guī)定CP′=0.
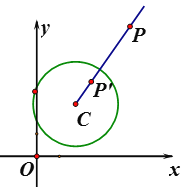
根據(jù)上述材料,請你解決以下問題:
(1)當⊙O的半徑為1時,
①在點![]() 關于⊙O的發(fā)散點的是點 ;其對應發(fā)散點的坐標是 ;
關于⊙O的發(fā)散點的是點 ;其對應發(fā)散點的坐標是 ;
②點P在直線![]() 上,若點P關于⊙O的發(fā)散點P′存在,且點P′不在x軸上,求點P的橫坐標m的取值范圍;
上,若點P關于⊙O的發(fā)散點P′存在,且點P′不在x軸上,求點P的橫坐標m的取值范圍;
(2)⊙C的圓心C在x軸上,半徑為1,直線![]() 與x軸、y軸分別交于點A,B.若線段AB上存在點P,使得點P關于⊙C的發(fā)散點P′在⊙C的內部,請直接寫出圓心C的橫坐標n的取值范圍 .
與x軸、y軸分別交于點A,B.若線段AB上存在點P,使得點P關于⊙C的發(fā)散點P′在⊙C的內部,請直接寫出圓心C的橫坐標n的取值范圍 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】問題情境:如圖1,在正方形ABCD中,E為邊BC上一點(不與點B、C重合),垂直于AE的一條直線MN分別交AB、AE、CD于點M、P、N.判斷線段DN、MB、EC之間的數(shù)量關系,并說明理由.
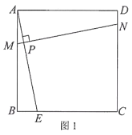
問題探究:在“問題情境”的基礎上,
(1)如圖2,若垂足P恰好為AE的中點,連接BD,交MN于點Q,連接EQ,并延長交邊AD于點F.求∠AEF的度數(shù);
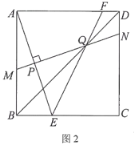
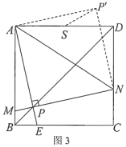
(2)如圖3,當垂足P在正方形ABCD的對角線BD上時,連接AN,將△APN沿著AN翻折,點P落在點P'處.若正方形ABCD的邊長為4 ,AD的中點為S,求P'S的最小值.
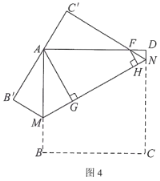
問題拓展:如圖4,在邊長為4的正方形ABCD中,點M、N分別為邊AB、CD上的點,將正方形ABCD沿著MN翻折,使得BC的對應邊B'C'恰好經(jīng)過點A,C'N交AD于點F.分別過點A、F作AG⊥MN,FH⊥MN,垂足分別為G、H.若AG=![]() ,請直接寫出FH的長.
,請直接寫出FH的長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
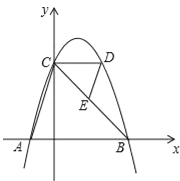
【題目】如圖,拋物線y=﹣(x﹣1)2+4與x軸交于點A,B(點A在點B的左側),與y軸交于點C,CD∥x軸交拋物線于另一點D,連結AC,DE∥AC交邊CB于點E.
(1)求A,B兩點的坐標;
(2)求△CDE與△BAC的面積之比.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】下列圖形都是由同樣大小的菱形按照一定規(guī)律組成的,請根據(jù)排列規(guī)律完成下列問題:
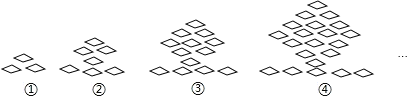
(1)填寫下表:
圖形序號 | 菱形個數(shù) |
| 3 |
| 7 |
| ______ |
| ______ |
|
|
(2)根據(jù)表中規(guī)律猜想,圖n中菱形的個數(shù)![]() 用含n的式子表示,不用說理
用含n的式子表示,不用說理![]() ;
;
(3)是否存在一個圖形恰好由91個菱形組成?若存在,求出圖形的序號;若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為紀念建國70周年,某校舉行班級歌詠比賽,歌曲有:《我愛你,中國》,《歌唱祖國》,《我和我的祖國》(分別用字母A,B,C依次表示這三首歌曲).比賽時,將A,B,C這三個字母分別寫在3張無差別不透明的卡片正面上,洗勻后正面向下放在桌面上,八(1)班班長先從中隨機抽取一張卡片,放回后洗勻,再由八(2)班班長從中隨機抽取一張卡片,進行歌詠比賽.
(1)八(1)班抽中歌曲《我和我的祖國》的概率是__________;
(2)試用畫樹狀圖或列表的方法表示所有可能的結果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
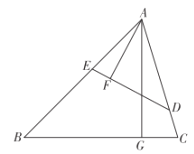
【題目】如圖,在銳角三角形ABC中,點D,E分別在邊AC,AB上,AG⊥BC于點G,AF⊥DE于點F,∠EAF=∠GAC.
(1)求證ΔADE∽ΔABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com