
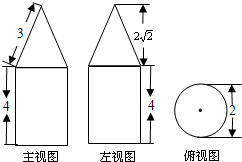
 如右圖是某幾何體的三視圖及相關數據,則該幾何體的表面積是
如右圖是某幾何體的三視圖及相關數據,則該幾何體的表面積是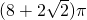
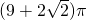
 LR,扇形的弧長為底面圓的周長,扇形的半徑為圓錐的母線長;圓柱側面積等于展開后矩形的面積,矩形的長為圓柱的高,寬為底面圓的周長;而該幾何體的表面積=圓錐的側面積+圓柱的側面積+圓柱的底面積.
LR,扇形的弧長為底面圓的周長,扇形的半徑為圓錐的母線長;圓柱側面積等于展開后矩形的面積,矩形的長為圓柱的高,寬為底面圓的周長;而該幾何體的表面積=圓錐的側面積+圓柱的側面積+圓柱的底面積. •2π•1•3=3π,
•2π•1•3=3π,

 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com