
【題目】(8分)如圖,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于點E,交AC于點F,過點E作EG//BC交AC于點G.(1)求證: AE=AF; (2)若AG=4,AC=7,求FG的長.

【答案】(1)見解析;(2)1.
【解析】分析:(1)由角平分線的定義和已知條件證出∠AFB=∠AEF,即可得出結論;(2)由SAS證明:△ABF≌△HBF,得出AF=FH,∠AFB=∠HFB,再證明1△AEG≌△FHC,得出AG=FC=4,即可得出結果.
本題解析:
(1)∵BF平分∠ABC
∴∠ABF=∠CBF
∵∠AFB=180°-∠ABF-∠BAF
∠BED=180°-∠CBF-∠ADB
又∵∠BAC=∠ADB
∴∠AFB=∠BED
∵∠AEF=∠BED
∴∠AFB=∠AEF
∴AE=AF
(2)如圖,在BC上截取BH=AB,連接FH
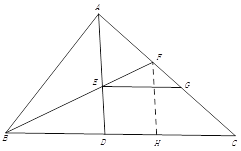
在△ABF和△HBF中
∵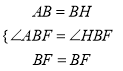
∴△ABF≌△HBF(SAS)
∴AF=FH,∠AFB=∠HFB
∵∠AFB=∠AEF
∴∠HFB=∠AEF
∴AE∥FH
∴∠GAE=∠CFH
∵EG∥BC
∴∠AGE=∠C
∵AE=AF
∴AE=FH
在△AEG和△FHC中
∵
∴△AEG≌△FHC(AAS)
∴AG=FC=4
∴FG=AG+ FC -AC=1


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案科目:初中數學 來源: 題型:
【題目】已知a,b,c是△ABC的三條邊長,化簡|a+b﹣c|+|b﹣a﹣c|的結果為( )
A.2a+2bB.2a+2b﹣2cC.2b﹣2cD.2a
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如下表,從左到右在每個小格子中都填入一個整數,使得其中任意三個相鄰格子中所填整數之和都相等,則第2011個格子中的數為 ( )
![]()
A. 3 B. 2 C. 0 D. -1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,半徑為1個單位的圓片上有一點A與數軸上的原點重合,AB是圓片的直徑.

(1)把圓片沿數軸向左滾動1周,點B到達數軸上點C的位置,點C表示的數是
__________數(填“無理”或“有理”),這個數是__________.
(2)把圓片沿數軸滾動2周,點A到達數軸上點D的位置,點D表示的數是__________.
(3)圓片在數軸上向右滾動的周數記為正數,圓片在數軸上向左滾動的周數記為負數,依次運動情況記錄如下:+2,-1,+3,-4,-3
①第幾次滾動后,A點距離原點最近?第幾次滾動后,A點距離原點最遠?
②當圓片結束運動時,A點運動的路程共有多少?此時點A所表示的數是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com