Question

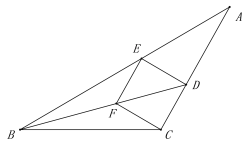
【題目】如圖，在△ABC中，AC=BC=6,∠ACB＞90°,∠ABC的平分線交AC于點D，E是AB上一點，且BE=BC，CF∥ED交BD于點F，連接EF,ED.

（1）求證：四邊形CDEF是菱形．

（2）當∠ACB＝ 度時，四邊形CDEF是正方形，請給予證明；并求此時正方形的邊長。

Answer 1

【答案】（1）詳見解析；（2）當∠ACB＝120度時，四邊形CDEF是正方形，證明見解析，此時正方形的邊長為 .

【解析】

（1）先證△CBD≌△EBD，由全等三角形的性質得DE=DC，∠BDC=∠BDE，同理△BCF≌△BEF，EF=CF，再根據平行線的性質得∠CFD=∠BDE，等量代換得CFD=∠BDC，可得CF=CD，根據四邊相等的四邊形是菱形可得結論；

（2）當∠ACB＝120度時，四邊形CDEF是正方形.由等腰三角形的性質可得∠A=∠ABC=30°，由角平分線得∠CBD=∠EBD=15°，根據平行線的性質得∠BEF=∠A=30°，再由三角形外角的性質可得∠EFD=∠EBD+∠BEF=45°，由菱形的性質可證出∠EFD=∠EDF=45°，則∠FED=90°，菱形CDEF是正方形；設正方形CDEF的邊長為x，在Rt△ADE中，利用30°角的直角三角形的性質表示出AD=x，由AB=AC=6可得AD=6-x,則6-x =x，解方程即可求得正方形的邊長.

（1）證明：∵BD平分∠ABC

∴∠CBD=∠EBD，

在△CBD和△EBD中

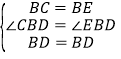∴△CBD≌△EBD（SAS）

∴DE=DC，∠BDC=∠BDE

同理△BCF≌△BEF

∴EF=CF

∵CF∥ED ∴∠CFD=∠BDE

∴∠CFD=∠BDC

∴CF=CD

∴EF=CF=CD=DE

∴四邊形CDEF是菱形

（2）當∠ACB＝ 120 度時，四邊形CDEF是正方形

證明：∵AC=BC ∠ACB＝ 120°

∴∠A=∠ABC=30°

∵BD平分∠ABC

∴∠CBD=∠EBD=15°

∵四邊形CDEF是菱形

∴EF∥AC

∴∠BEF=∠A=30°

∴∠EFD=∠EBD+∠BEF=15°+30°=45°,

∵EF=ED

∴∠EFD=∠EDF=45°

∴∠FED=90°

∴菱形CDEF是正方形.

設正方形CDEF的邊長為x，

在Rt△ADE中，∠A=30° ∴AE=2x, AD=,

∵AD+CD=AC=6

∴+x=6 ∴x=

∴正方形CDEF的邊長為.

故答案為：（1）詳見解析；（2）當∠ACB＝120度時，四邊形CDEF是正方形，證明見解析，此時正方形的邊長為 .