某小企業計劃投資A、B兩類產品的生產,據市場調查:A類是傳統產品,投資x(萬元)的實際收益是yA=24%x(萬元);B類是新科技產品,同樣投資x(萬元)在相同的時間內的毛收益是10%x2(萬元),但需支付毛收益的20%作為專利費;并且,根據有關市場預測機構的風險提示,投資B類的投資額不能超過投資A類的投資額的2倍;
(1)寫出投資B類產品的實際收益yB(萬元)與投資x(萬元)的函數關系式;
(2)若同樣投資x(萬元)生產兩類產品,當x為多少時,兩種產品的實際收益相同?
(3)若企業共有30(萬元)資金分別投資這兩類產品,如何投資才能使總的實際收益最大?最大收益是多少(萬元)?
【答案】
分析:(1)根據條件中的數量關系可以直接求出函數關系式.
(2)根據解析式建立方程求出其解就可以了.
(3)根據總收益等于兩類產品收益之和就可以設實際總收益為W,建立一個解析式就可以求出其值.
解答:解:(1)由題意,得
y
B=10%x
2(1-20%),
=8%x
2.
(2)由題意,得
8%x
2=24%x,
解得:x
1=0(不符合題意),x
2=3.
∴當投資3萬元生產兩類產品,兩種產品的實際收益相同.
(3)設實際總收益為W萬元,有a萬元投資A產品,有(30-a)投資B產品,由題意,得
W=8%(30-a)
2+24%a,
=8%(a-
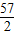
)
2+7.02,
∵a>0,拋物線的開口向上,
∴在對稱軸左側,y隨x減小而增大,
∴投資B類的投資額不能超過投資A類的投資額的2倍,
∴最少投資A類a=10萬元,W
最大=34.4萬元.
點評:本題考查了一次函數的解析式,解一元二次方程,二次函數的頂點式的運用,在解答時根據條件建立適當的函數關系式是解答此類問題的關鍵.

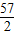 )2+7.02,
)2+7.02,
